
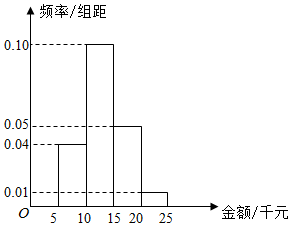
 ij����Ӫ������Ϊ��ͳ��ij������2015��11��11����ij���������������������˸���100�����ѵ��������������õ���ͼƵ�ʷֲ�ֱ��ͼ��
ij����Ӫ������Ϊ��ͳ��ij������2015��11��11����ij���������������������˸���100�����ѵ��������������õ���ͼƵ�ʷֲ�ֱ��ͼ������ ��1������λ����x����Ƶ�ʷֲ�ֱ��ͼ�������ܹ���ֱ��ͼ������������λ����
��2�������⣬��ȫ����ȡ�������С��������ˡ�����������B��3��0.3��������X����ȡֵΪ1��3���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к���ѧ������
��� �⣺��1������λ����x��
����Ƶ�ʷֲ�ֱ��ͼ�����ʵã�
5��0.04+��x-10����0.1=0.5��
���x=13��
�����ֱ��ͼ������������λ��Ϊ13������4�֣�
��2�������⣬��ȫ����ȡ�������С��������ˡ�����������B��3��0.3����
����X����ȡֵΪ1��3��
��$P��X=3��=C_3^3{0.3^3}+C_3^0{0.7^3}=0.37$������6�֣�
$P��X=1��=C_3^1{0.3^1}•{0.7^2}+C_3^2{0.3^2}•{0.7^1}=0.63$����8�֣�
����X�ķֲ���Ϊ
| X | 1 | 3 |
| P | 0.63 | 0.37 |
���� ���⿼����λ������������ɢ����������ķֲ��м���ѧ�����������е��⣬����ʱҪ�������⣬ע�����ֲ������ʵĺ������ã�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ?x��Z��ex��1 | B�� | ?x∉Z��ex��1 | C�� | ?x��Z��ex��1 | D�� | ?x∉Z��ex��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com