
分析 利用向量垂直的条件,得出x+2y=1,利用“1”的代换,结合基本不等式,即可得出结论.
解答 解:∵$\overrightarrow a$=(x-1,y),$\overrightarrow b$=(1,2),且$\overrightarrow a$⊥$\overrightarrow b$,
∴$\overrightarrow a$•$\overrightarrow b$=x-1+2y=0,
∴x+2y=1,
∵x>0,y>0,
∴$\frac{1}{x}$+$\frac{1}{y}$=($\frac{1}{x}$+$\frac{1}{y}$)(x+2y)=3+$\frac{2y}{x}$+$\frac{x}{y}$≥3+2$\sqrt{2}$,当且仅当$\frac{2y}{x}$=$\frac{x}{y}$时取等号,
∴$\frac{1}{x}$+$\frac{1}{y}$的最小值为3+2$\sqrt{2}$,
故答案为:3+2$\sqrt{2}$.
点评 本题考查向量垂直的条件,考查基本不等式的运用,正确运用“1”的代换是关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
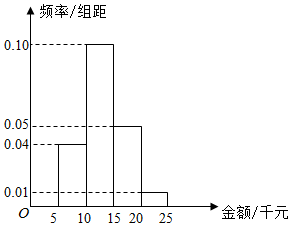 某网络营销部门为了统计某市网友2015年11月11日在某网店的网购情况,随机抽查了该市100名网友的网购金额情况,得到如图频率分布直方图.
某网络营销部门为了统计某市网友2015年11月11日在某网店的网购情况,随机抽查了该市100名网友的网购金额情况,得到如图频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com