
分析 根据同角的三角函数的关系进行化简,然后代值求解即可得答案.
解答 解:$\frac{cos(α-\frac{7π}{2})+2sin(3π-α)}{csc(3π+α)+sec(\frac{5π}{2}+α)}$=$\frac{cos(4π-\frac{π}{2}+α)+2sin(2π+π-α)}{\frac{1}{sin(2π+π+α)}+\frac{1}{cos(2π+\frac{π}{2}+α)}}$
=$\frac{sinα+2sinα}{-\frac{1}{sinα}-\frac{1}{sinα}}$=$-\frac{3}{2}si{n}^{2}α$=$-\frac{3}{2}(1-co{s}^{2}α)=-\frac{3}{2}×\frac{16}{25}=-\frac{24}{25}$.
点评 本题考查了诱导公式的应用,以及同角三角函数间的基本关系,熟练掌握公式及基本关系是解本题的关键,是基础题.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
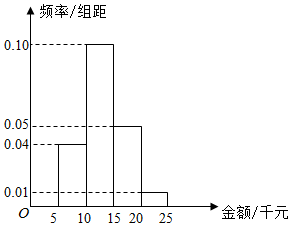 某网络营销部门为了统计某市网友2015年11月11日在某网店的网购情况,随机抽查了该市100名网友的网购金额情况,得到如图频率分布直方图.
某网络营销部门为了统计某市网友2015年11月11日在某网店的网购情况,随机抽查了该市100名网友的网购金额情况,得到如图频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $-\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $-\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
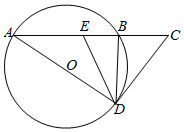 如图,A,B是圆O上两点,延长AB至点C,满足AB=2BC=2,过C作直线CD与圆O相切于点D,∠ADB的平分线交AB于点E.
如图,A,B是圆O上两点,延长AB至点C,满足AB=2BC=2,过C作直线CD与圆O相切于点D,∠ADB的平分线交AB于点E.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com