
(本小题满分13分)时下,网校教学越来越受到广大学生的喜爱,它已经成为学生们课外学习的一种趋势,假设某网校的套题每日的销售量 (单位:千套)与销售价格
(单位:千套)与销售价格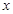 (单位:元/套)满足的关系式
(单位:元/套)满足的关系式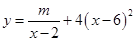 ,其中
,其中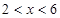 ,
,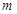 为常数.已知销售价格为4元/套时,每日可售出套题21千套.
为常数.已知销售价格为4元/套时,每日可售出套题21千套.
(1)求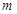 的值;
的值;
(2)假设网校的员工工资,办公等所有开销折合为每套题2元(只考虑销售出的套数),试确定销售价格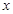 的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
(本小题共12分)
已知函数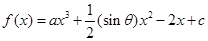 的图象过点
的图象过点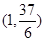 ,且在
,且在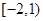 内单调递减,在
内单调递减,在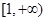 上单调递增。
上单调递增。
(1)求 的解析式;
的解析式;
(2)若对于任意的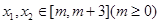 ,不等式
,不等式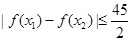 恒成立,试问这样的
恒成立,试问这样的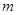 是否存在.若存在,请求出
是否存在.若存在,请求出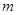 的范围,若不存在,说明理由;
的范围,若不存在,说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分))
京广高铁于2012年12月26日全线开通运营,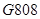 次列车在平直的铁轨上匀速行驶,由于遇到紧急情况,紧急刹车时列车行驶的路程
次列车在平直的铁轨上匀速行驶,由于遇到紧急情况,紧急刹车时列车行驶的路程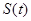 (单位:
(单位: )和时间
)和时间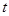 (单位:
(单位: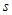 )的关系为:
)的关系为: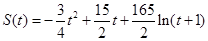 .
.
(1)求从开始紧急刹车至列车完全停止所经过的时间;
(2)求列车正常行驶的速度;
(3)求紧急刹车后列车加速度绝对值的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有一批运动服装原价为每套80元,两个商场均有销售,为了吸引顾客,两商场纷纷推出优惠政策。甲商场的优惠办法是:买一套减4元,买两套每套减8元,买三套每套减12元,......,依此类推,直到减到半价为止;乙商场的优惠办法是:一律7折。某单位欲为每位员工买一套运动服装,问选择哪个商场购买更省钱?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知函数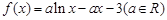 .
.
(I)当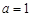 时,求函数
时,求函数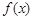 的单调区间;
的单调区间;
(II)若函数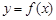 的图象在点
的图象在点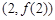 处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的
处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的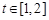 ,函数
,函数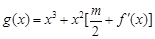 在区间
在区间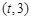 上总存在极值?
上总存在极值?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某汽车生产企业上年度生产一品牌汽车的投入成本为10万元/辆,出厂价为13万元/辆,年销售量为5000辆.本年度为适应市场需求,计划提高产品档次,适当增加投入成本,若每辆车投入成本增加的比例为 (0<
(0< <1
<1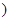 ,则出厂价相应提高的比例为0.7
,则出厂价相应提高的比例为0.7 ,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
(1)若年销售量增加的比例为0.4 ,为使本年度的年利润比上年度有所增加,则投入成本增加的比例
,为使本年度的年利润比上年度有所增加,则投入成本增加的比例 应在什么范围内?
应在什么范围内?
(2)年销售量关于 的函数为
的函数为 ,则当
,则当 为何值时,本年度的年利润最大?最大利润为多少?
为何值时,本年度的年利润最大?最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题12分)
提高过立交桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,成都某立交桥上的车流速度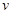 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当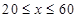 时,车流速度
时,车流速度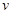 是车流密度
是车流密度 的一次函数.
的一次函数.
(Ⅰ)当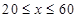 时,求函数
时,求函数 的表达式;
的表达式;
(Ⅱ)当车流密度 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)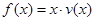 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com