
某汽车生产企业上年度生产一品牌汽车的投入成本为10万元/辆,出厂价为13万元/辆,年销售量为5000辆.本年度为适应市场需求,计划提高产品档次,适当增加投入成本,若每辆车投入成本增加的比例为 (0<
(0< <1
<1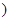 ,则出厂价相应提高的比例为0.7
,则出厂价相应提高的比例为0.7 ,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
(1)若年销售量增加的比例为0.4 ,为使本年度的年利润比上年度有所增加,则投入成本增加的比例
,为使本年度的年利润比上年度有所增加,则投入成本增加的比例 应在什么范围内?
应在什么范围内?
(2)年销售量关于 的函数为
的函数为 ,则当
,则当 为何值时,本年度的年利润最大?最大利润为多少?
为何值时,本年度的年利润最大?最大利润为多少?
(1)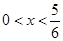 ;(2)当
;(2)当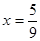 时,本年度的年利润最大,最大利润为20000万元.
时,本年度的年利润最大,最大利润为20000万元.
解析试题分析:(1)由题意得:本年度每辆车的投入成本为10×(1+x);
出厂价为13×(1+0.7x);年销售量为5000×(1+0.4x), 2分
因此本年度的利润为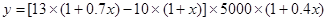
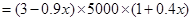
即: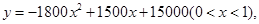 6分
6分
由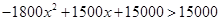 , 得
, 得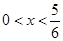 8分
8分
(2)本年度的利润为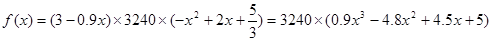
则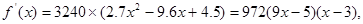 10分
10分
由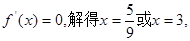
当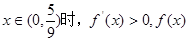 是增函数;当
是增函数;当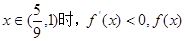 是减函数.
是减函数.
∴当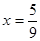 时,
时,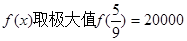 万元, 12分
万元, 12分
因为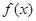 在(0,1)上只有一个极大值,所以它是最大值, 14分
在(0,1)上只有一个极大值,所以它是最大值, 14分
所以当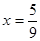 时,本年度的年利润最大,最大利润为20000万元. 16分
时,本年度的年利润最大,最大利润为20000万元. 16分
考点:函数的实际应用题;利用导数研究函数的单调区间、极值和最值。
点评:研究数学模型,建立数学模型,进而借鉴数学模型,对提高解决实际问题的能力,以及提高数学素养都是十分重要的.建立模型的步骤可分为: (1) 分析问题中哪些是变量,哪些是常量,分别用字母表示; (2) 根据所给条件,运用数学知识,确定等量关系; (3) 写出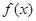 的解析式并指明定义域。
的解析式并指明定义域。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
(本小题满分13分)时下,网校教学越来越受到广大学生的喜爱,它已经成为学生们课外学习的一种趋势,假设某网校的套题每日的销售量 (单位:千套)与销售价格
(单位:千套)与销售价格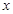 (单位:元/套)满足的关系式
(单位:元/套)满足的关系式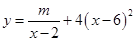 ,其中
,其中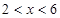 ,
,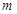 为常数.已知销售价格为4元/套时,每日可售出套题21千套.
为常数.已知销售价格为4元/套时,每日可售出套题21千套.
(1)求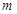 的值;
的值;
(2)假设网校的员工工资,办公等所有开销折合为每套题2元(只考虑销售出的套数),试确定销售价格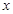 的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题14分)如图,一水渠的横断面是抛物线形,O是抛物线的顶点,口宽EF=4米,高3米,建立适当的直角坐标系,(1)求抛物线方程.(2)若将水渠横断面改造成等腰梯形ABCD,要求高度不变,只挖土,不填土,求梯形ABCD的下底AB多大时,所挖的土最少? 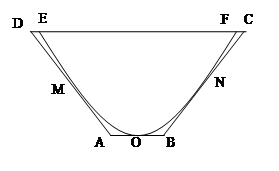
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数 的最小值为1,且
的最小值为1,且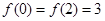 。
。
(1)求 的解析式;
的解析式;
(2)若 在区间
在区间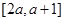 上不单调,求实数
上不单调,求实数 的取值范围;
的取值范围;
(3)在区间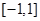 上,
上,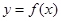 的图象恒在
的图象恒在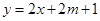 的图象上方,试确定实数
的图象上方,试确定实数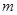 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com