
| A. | 外心 | B. | 重心 | C. | 内心 | D. | 垂心 |
分析 作出三个二面角,利用三角形全等得出O到△ABC的三边距离相等,得出结论.
解答  解:设P在底面ABC的射影为O,过O向△ABC的三边作垂线OD,OE,OF,
解:设P在底面ABC的射影为O,过O向△ABC的三边作垂线OD,OE,OF,
连结PD,PE,PF,
∵PO⊥平面ABC,AB?平面ABC,
∴PO⊥AB,又OD⊥AB,OD∩OP=O,
∴AB⊥平面OPD,∴AB⊥PD,
∴∠PDO为侧面PAB与平面ABC的二面角,
同理∠PEO,∠PFO为其余两侧面与底面ABC的二面角,
∴∠PDO=∠PEO=∠PFO,
又PO⊥OD,PO⊥OE,PO⊥OF,PO为公共边,
∴Rt△POD≌Rt△POE≌Rt△POF,
∴OD=OE=OF,
∴O是△ABC的内心.
故选C.
点评 本题考查了棱锥的结构特征,线面垂直的判定,二面角的做法,属于中档题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e2017•f(2017)>f(0) | B. | e2017•f(2017)=f(0) | ||
| C. | e2017•f(2017)<f(0) | D. | e2017f(2017)与f(0)的大小无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
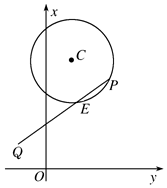 如图,已知圆C:x2+y2-4x-14y+45=0及点Q(-2,3)
如图,已知圆C:x2+y2-4x-14y+45=0及点Q(-2,3)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com