Question

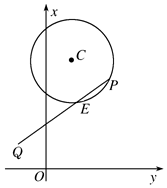
3．如图，已知圆C：x²+y²-4x-14y+45=0及点Q（-2，3）
（1）若点P（m，m+1）在圆C上，求直线PQ的斜率以及直线PQ与圆C的相交弦PE的长度；
（2）若N（x，y）是直线x+y+1=0上任意一点，过N作圆C的切线，切点为A，当切线长|NA|最小时，求N点的坐标，并求出这个最小值．
（3）若M（x，y）是圆上任意一点，求$\frac{y-3}{x+2}$的最大值和最小值．

Answer 1

分析 （1）通过点P（m，m+1）在圆C上，求出m=4，推出P的坐标，求出直线PQ的斜率，得到直线PQ的方程，利用圆心（2，7）到直线的距离d，求解即可．
（2）判断当NC最小时，NA最小，结合当NC⊥l时，NC最小，求出|NC|的最小值，然后求解直线方程．
（3）利用k_MQ=$\frac{y-3}{x+2}$，题目所求即为直线MQ的斜率k的最值，且当直线MQ为圆的切线时，斜率取最值．设直线MQ的方程为y-3=k（x+2），利用圆心到直线的距离求解即可．

解答 解：（1）∵点P（m，m+1）在圆C上，代入圆C的方程，解得m=4，∴P（4，5）
故直线PQ的斜率k=$\frac{5-3}{4-（-2）}$=$\frac{1}{3}$．因此直线PQ的方程为y-5=$\frac{1}{3}$（x-4）．
即x-3y+11=0，而圆心（2，7）到直线的距离d=$\frac{|2-3×7+11|}{\sqrt{10}}$=$\frac{8}{\sqrt{10}}$=$\frac{4\sqrt{10}}{5}$，
所以PE=2$\sqrt{{r}^{2}-{d}^{2}}$=$2\sqrt{8-（\frac{4\sqrt{10}}{5}）^{2}}$=$\frac{2\sqrt{40}}{5}$=$\frac{4\sqrt{10}}{5}$．…（4分）
（2）∵$|{NA}|=\sqrt{N{C^2}-{r^2}}=\sqrt{N{C^2}-8}$
∴当NC最小时，NA最小又知当NC⊥l时，NC最小，
∴$|{NC}|=d=2\sqrt{5}$…（6分）
⇒过C且与直线x+y+1=0垂直的直线方程：x-y+5=0，
∴N（-3，2）…（8分）
（3）∵k_MQ=$\frac{y-3}{x+2}$，
∴题目所求即为直线MQ的斜率k的最值，且当直线MQ为圆的切线时，斜率取最值．
设直线MQ的方程为y-3=k（x+2），即kx-y+2k+3=0．
当直线与圆相切时，圆心到直线的距离d=$\frac{|2k-7+2k+3|}{\sqrt{1+{k}^{2}}}$=r=2 $\sqrt{2}$．
两边平方，即（4k-4）²=8（1+k²），解得k=2-$\sqrt{3}$，或k=2+$\sqrt{3}$．
所以$\frac{y-3}{x+2}$的最大值和最小值分别为2+$\sqrt{3}$和2-$\sqrt{3}$．…（12分）

点评 本题考查直线与圆的位置关系的综合应用，考查转化思想以及计算能力．