
分析 (1)依题意${a_2}=\frac{1}{4}{a_1}+p=\frac{1}{4}+p=1$,$p=\frac{3}{4}$;
(2)由条件得${a_2}-{a_1}=\frac{1}{4}{a_1}^2+p-{a_1}=p-\frac{3}{4}>0$得a2>a1,由${a_{n+2}}=\frac{1}{4}{a_{n+1}}^2+p,{a_{n+1}}=\frac{1}{4}{a_n}^2+p$,两式相减得${a_{n+2}}-{a_{n+1}}=\frac{1}{4}{a_{n+1}}^2-\frac{1}{4}{a_n}^2=\frac{1}{4}({{a_{n+1}}^2-{a_n}^2})=\frac{1}{4}({{a_{n+1}}-{a_n}})({{a_{n+1}}+{a_n}})$即可判定.
(3)由${a_{k+1}}-{a_k}=\frac{1}{4}{a_k}^2-{a_k}+p=\frac{1}{4}{({{a_k}-2})^2}+p-1≥p-1$,得an=a1+(a2-a1)+…(an-an-1)>1+(n-1)(p-1),即可得,当p>1时,an越来越大,不满足an<2,所以要使得an<2对一切整数n恒成立,只可能p≤1,用数学归纳法证明当p=1时,an<2恒成立即可.
解答 解:(1)若数列{an}是常数列,则${a_2}=\frac{1}{4}{a_1}+p=\frac{1}{4}+p=1$,$p=\frac{3}{4}$;显然,当$p=\frac{3}{4}$时,有an=1
(2)由条件得${a_2}-{a_1}=\frac{1}{4}{a_1}^2+p-{a_1}=p-\frac{3}{4}>0$得a2>a1,
又因为${a_{n+2}}=\frac{1}{4}{a_{n+1}}^2+p,{a_{n+1}}=\frac{1}{4}{a_n}^2+p$,
两式相减得${a_{n+2}}-{a_{n+1}}=\frac{1}{4}{a_{n+1}}^2-\frac{1}{4}{a_n}^2=\frac{1}{4}({{a_{n+1}}^2-{a_n}^2})=\frac{1}{4}({{a_{n+1}}-{a_n}})({{a_{n+1}}+{a_n}})$
显然有an>0,所以an+2-an+1与an+1-an同号,而a2-a1>0,所以an+1-an>0;
从而有an<an+1.
(3)因为${a_{k+1}}-{a_k}=\frac{1}{4}{a_k}^2-{a_k}+p=\frac{1}{4}{({{a_k}-2})^2}+p-1≥p-1$,
所以an=a1+(a2-a1)+…(an-an-1)>1+(n-1)(p-1),
这说明,当p>1时,an越来越大,不满足an<2,所以要使得an<2对一切整数n恒成立,只可能p≤1,
下面证明当p=1时,an<2恒成立;用数学归纳法证明:
当n=1时,a1=1显然成立;
假设当n=k时成立,即ak<2,
则当n=k+1时,${a_{k+1}}=\frac{1}{4}{a_k}^2+1<\frac{1}{4}×{2^2}+1=2$成立,
由上可知对一切正整数n恒成立,因此,正数p的最大值是1
点评 本题考查了数列的递推式,数列与不等式,数学归纳法,属于难题.


 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:解答题
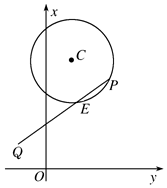 如图,已知圆C:x2+y2-4x-14y+45=0及点Q(-2,3)
如图,已知圆C:x2+y2-4x-14y+45=0及点Q(-2,3)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x1,x2∈R,(f(x1)-f(x2))(x1-x2)>0 | B. | ?x1,x2∈R,(f(x1)-f(x2))(x1-x2)≥0 | ||
| C. | ?x1,x2∈R,(f(x1)-f(x2))(x1-x2)≥0 | D. | ?x1,x2∈R,(f(x1)-f(x2))(x1-x2)<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$ | B. | $\frac{\sqrt{41}}{4}$ | C. | $\frac{5}{4}$ | D. | $\frac{\sqrt{41}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8π | B. | 16π | C. | 24π | D. | 32π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com