
分析 △ABD和△BCD的形状寻找截面圆心位置,从而得出球心位置.计算外接球的半径即可得出面积.
解答  解:∵空间四边形ABCD中,AB=BD=AD=2,∴△ABD是正三角形;
解:∵空间四边形ABCD中,AB=BD=AD=2,∴△ABD是正三角形;
又BC=1,$CD=\sqrt{3}$,∴△BCD是直角三角形;
取BD的中点M,连接CM,则AM⊥BD,
又平面ABD⊥平面BCD,∴AM⊥平面BCD,
∴棱锥外接球的球心为△ABD的中心,
∵AM=$\sqrt{A{B}^{2}-B{M}^{2}}$=$\sqrt{3}$,
∴该四棱锥A-BCD的外接球的半径为$\frac{2}{3}AM$=$\frac{2\sqrt{3}}{3}$,
∴几何体外接球的表面积S=4π($\frac{2\sqrt{3}}{3}$)2=$\frac{16π}{3}$.
故答案为:$\frac{16π}{3}$.
点评 本题考查了棱锥与外接球的位置关系,属于中档题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $C_7^5A_{10}^5A_5^5$种 | B. | $A_7^5C_{10}^5A_5^5$种 | ||
| C. | $C_{10}^5C_7^5$种 | D. | $C_7^5A_{10}^5$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
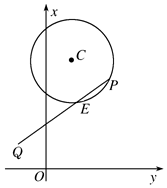 如图,已知圆C:x2+y2-4x-14y+45=0及点Q(-2,3)
如图,已知圆C:x2+y2-4x-14y+45=0及点Q(-2,3)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$ | B. | $\frac{\sqrt{41}}{4}$ | C. | $\frac{5}{4}$ | D. | $\frac{\sqrt{41}}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com