
分析 根据物理学知识,直线BC一定过(-1,6)关于y轴的对称点(1,6),直线AB一定过(1,6)关于x轴的对称点(1,-6)且kAB=kCD,即可求出AB方程,CD方程,求出点B,C坐标,可得直线BC的方程.
解答 解:如图所示,由题设,点B在原点O的左侧,根据物理学知识,直线BC一定过(-1,6)关于y轴的对称点(1,6),直线AB一定过(1,6)关于x轴的对称点(1,-6)且kAB=kCD,
∴kAB=kCD=$\frac{4+6}{-3-1}$=-$\frac{5}{2}$.
∴AB方程为y-4=-$\frac{5}{2}$(x+3).
令y=0,得x=-$\frac{7}{5}$,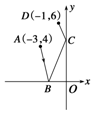
∴B($-\frac{7}{5}$,0)
CD方程为y-6=-$\frac{5}{2}$(x+1).
令x=0,得y=$\frac{7}{2}$,
∴C(0,$\frac{7}{2}$)
∴BC的方程为$\frac{x}{-\frac{7}{5}}$+$\frac{y}{\frac{7}{2}}$=1,
故得BC的一般方程为:5x-2y+7=0.
点评 本题考查了直线关于点对称的直线方程的求法,考查了斜率公式的运用,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4) | B. | (-∞,1)∪(1,4] | C. | (0,4) | D. | R |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 12 | C. | 15 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∵a>b(a,b∈R),∴a+2i>b+2i(i是虚数单位) | |
| B. | 若f(x)是增函数,则f'(x)>0 | |
| C. | 若α,β是锐角△ABC的两个内角,则sinα>cosβ | |
| D. | 若A是△ABC的内角,且cosA>0,则△ABC为锐角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | c<b<a | C. | c<a<b | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com