
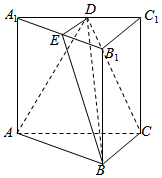
 在三棱柱ABC-A1B1C1中,A1A⊥平面ABC,AC⊥BC,BC=C1C=AC=2,D是A1C1上的一点,E是A1B1的中点,C1D=kA1C1.
在三棱柱ABC-A1B1C1中,A1A⊥平面ABC,AC⊥BC,BC=C1C=AC=2,D是A1C1上的一点,E是A1B1的中点,C1D=kA1C1.分析 (Ⅰ)由题意可知,k=$\frac{1}{2}$时,B,C,D,E四点共面.然后利用三角形中位线定理可知DE∥B1C1,再由B1C1∥BC,得DE∥BC,由此说明B,C,D,E四点共面;
(Ⅱ)在三棱锥A-BCD中,利用等积法求出点A到平面BCDE的距离h,然后代入四棱锥的体积公式求得答案.
解答 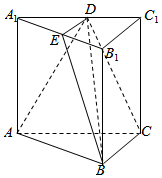 解:(Ⅰ)当k=$\frac{1}{2}$时,B,C,D,E四点共面.
解:(Ⅰ)当k=$\frac{1}{2}$时,B,C,D,E四点共面.
事实上,若k=$\frac{1}{2}$,则D是A1C1的中点,
又E是A1B1的中点,∴DE∥B1C1,
又B1C1∥BC,∴DE∥BC,则B,C,D,E四点共面;
(Ⅱ) 在(Ⅰ)的条件下,即D为A1C1的中点,
又A1A⊥平面ABC,A1ACC1是矩形,
此时,$CD=\sqrt{{C_1}{C^2}+{C_1}{D^2}}=\sqrt{{2^2}+{1^2}}=\sqrt{5}$,
又A1A⊥平面ABC,∴BC⊥A1A,又BC⊥AC,
∴BC⊥平面ACD,由VA-BCD=VB-ACD,
设点A到平面BCDE的距离h,则$\frac{1}{3}•\frac{1}{2}BC•CD•h=\frac{1}{3}•\frac{1}{2}BC•AC•{A_1}A$,
∴$h=\frac{AC•{A_1}A}{CD}=\frac{2•2}{{\sqrt{5}}}=\frac{{4\sqrt{5}}}{5}$,
则${V_{A-BCDE}}=\frac{1}{3}•\frac{1}{2}•({BC+DE})•CD•h$=$\frac{1}{6}•({2+1})\sqrt{5}•\frac{{4\sqrt{5}}}{5}=2$.
点评 本题考查线面平行的判断,考查了棱锥体积的求法,训练了等积法,是中档题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
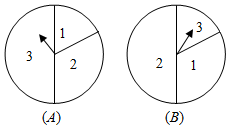 如图是两个独立的转盘(A)、(B),在两个图中三个扇形区域的圆心角分别为60°、120°、180°.用这两个转盘进行游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域为x,转盘(B)指针所对的区域为y,x、y∈{1,2,3},设x+y的值为ξ.
如图是两个独立的转盘(A)、(B),在两个图中三个扇形区域的圆心角分别为60°、120°、180°.用这两个转盘进行游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域为x,转盘(B)指针所对的区域为y,x、y∈{1,2,3},设x+y的值为ξ.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
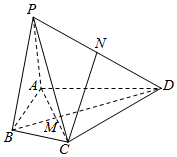 如图,在四棱锥P-ABCD中,△ACD是正三角形,BD垂直平分AC,垂足为M,∠ABC=120°,PA=AB=1,PD=2,N为PD的中点.
如图,在四棱锥P-ABCD中,△ACD是正三角形,BD垂直平分AC,垂足为M,∠ABC=120°,PA=AB=1,PD=2,N为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com