
已知过曲线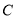 上任意一点
上任意一点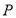 作直线
作直线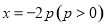 的垂线,垂足为
的垂线,垂足为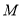 ,且
,且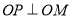 .
.
⑴求曲线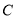 的方程;
的方程;
⑵设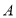 、
、 是曲线
是曲线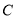 上两个不同点,直线
上两个不同点,直线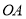 和
和 的倾斜角分别为
的倾斜角分别为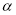 和
和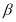 ,当
,当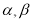 变化且
变化且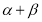 为定值
为定值 时,证明直线
时,证明直线 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
⑴
⑵当 时,直线
时,直线 恒过定点
恒过定点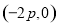 ,当
,当 时直线
时直线 恒过定点
恒过定点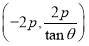 .
.
【解析】
试题分析:⑴要求曲线方程,但是不知道是哪种曲线,所以只能设点.根据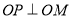 ,转化为
,转化为 求曲线方程即可;
求曲线方程即可;
⑵要证明直线恒过定点,必须得有直线方程,所以首先设出直线方程.又因为两个角是直线 和
和 的倾斜角,所以点
的倾斜角,所以点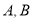 也得设出来.利用韦达定理,然后讨论
也得设出来.利用韦达定理,然后讨论 的范围变化,证明并得出定点坐标.
的范围变化,证明并得出定点坐标.
试题解析:⑴设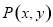 ,则
,则 ,由
,由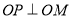 得
得 ,;
,;
即 ;所以轨迹方程为
;所以轨迹方程为 ;
;
⑵设 ,由题意得
,由题意得 (否则
(否则 )且
)且 ,
,
所以直线 的斜率存在,设其方程为
的斜率存在,设其方程为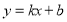 ,
,
因为 在抛物线上,所以
在抛物线上,所以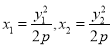 ,
,
将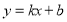 与
与 联立消去
联立消去 ,得
,得 ;
;
由韦达定理知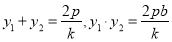 ①;
①;
(1)当 时,即
时,即 时,
时, ,所以
,所以 ,
,
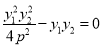 ,所以
,所以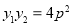 .由①知:
.由①知: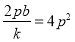 ,所以
,所以
因此直线 的方程可表示为
的方程可表示为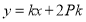 ,即
,即 .
.
所以直线 恒过定点
恒过定点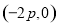
(2)当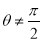 时,由
时,由 ,得
,得 =
= =
=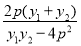
将①式代入上式整理化简可得: ,所以
,所以 ,
,
此时,直线 的方程可表示为
的方程可表示为
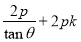 ,
,
即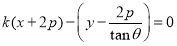 ,所以直线
,所以直线 恒过定点
恒过定点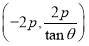 ;
;
所以由(1)(2)知,当 时,直线
时,直线 恒过定点
恒过定点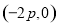 ,
,
当 时直线
时直线 恒过定点
恒过定点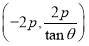 . 12分
. 12分
考点:相关点法求曲线方程;分类讨论.


科目:高中数学 来源:2015届新疆兵团农二师华山中学高二下学期期中文科数学试卷(解析版) 题型:选择题
某单位随机统计了某4天的用电量(度)与当天气温( )如下表,以了解二者的关系。
)如下表,以了解二者的关系。
气温( | 18 | 13 | 10 | -1 |
用电量(度) | 24 | 34 | 38 | 64 |
由表中数据得回归直线方程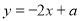 ,则
,则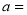
A.60 B.58 C.40 D.以上都不对
查看答案和解析>>
科目:高中数学 来源:2015届广西桂林十八中高二下学期开学考文科数学试卷(解析版) 题型:选择题
在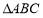 中,
中,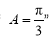 是
是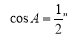 的( )
的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2015届广西桂林中学高二下学期期中考试理科数学试卷(解析版) 题型:填空题
在 类比此性质,如下图,在四面体P-ABC中,若PA、PB、PC两两垂直,底面ABC上的高为h,则得到的正确结论为__________________________.
类比此性质,如下图,在四面体P-ABC中,若PA、PB、PC两两垂直,底面ABC上的高为h,则得到的正确结论为__________________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com