
ЁОЬтФПЁПЯТБэЪЧФГаЃИпШ§вЛДЮдТПМ5ИіАрМЖЕФЪ§бЇЁЂЮяРэЕФЦНОљГЩМЈЃК
АрМЖ | 1 | 2 | 3 | 4 | 5 |
Ъ§бЇЃЈ | 111 | 113 | 119 | 125 | 127 |
ЮяРэЃЈ | 92 | 93 | 96 | 99 | 100 |
ЃЈЂёЃЉвЛАуРДЫЕЃЌбЇЩњЕФЮяРэГЩМЈгыЪ§бЇГЩМЈОпгаЯпадЯрЙиЙиЯЕЃЌИљОнЩЯБэЬсЙЉЕФЪ§ОнЃЌЧѓСНИіБфСП![]() ЃЌ
ЃЌ ![]() ЕФЯпадЛиЙщЗНГЬ
ЕФЯпадЛиЙщЗНГЬ![]() ЃЛ
ЃЛ
ЃЈЂђЃЉДгвдЩЯ5ИіАрМЖжаШЮбЁСНИіВЮМгФГЯюЛюЖЏЃЌЩшбЁГіЕФСНИіАрМЖжаЪ§бЇЦНОљЗждк115ЗжвдЩЯЕФИіЪ§ЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЗжВМСаКЭЪ§бЇЦкЭћ.
ЕФЗжВМСаКЭЪ§бЇЦкЭћ.
ИНЃК  ЃЌ
ЃЌ ![]()
ЁОД№АИЁПЃЈ1ЃЉ![]() ;ЃЈ2ЃЉМћНтЮі.
;ЃЈ2ЃЉМћНтЮі.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈЂёЃЉЗжБ№зіГіКсБъКЭзнБъЕФЦНОљЪ§ЃЌРћгУзюаЁЖўГЫЗЈзіГі![]() ЕФжЕЃЌдйЧѓГі
ЕФжЕЃЌдйЧѓГі![]() ЕФжЕЃЌаДГіЯпадЛиЙщЗНГЬЃЌЕУЕННсЙћЃЛЃЈЂђЃЉ
ЕФжЕЃЌаДГіЯпадЛиЙщЗНГЬЃЌЕУЕННсЙћЃЛЃЈЂђЃЉ ![]() ЕФПЩФмШЁжЕЗжБ№ЪЧ0ЃЌ1ЃЌ2ЃЌЧѓГіЯргІЕФИХТЪЃЌМДПЩЧѓ
ЕФПЩФмШЁжЕЗжБ№ЪЧ0ЃЌ1ЃЌ2ЃЌЧѓГіЯргІЕФИХТЪЃЌМДПЩЧѓ![]() ЕФЗжВМСаКЭЪ§бЇЦкЭћ.
ЕФЗжВМСаКЭЪ§бЇЦкЭћ.
ЪдЬтНтЮіЃКЃЈЂёЃЉгЩЬтвтЕУ![]() ЃЌ
ЃЌ ![]()
![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ 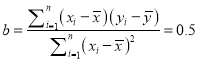 ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
ЙЪЫљЧѓЕФЛиЙщжБЯпЗНГЬЮЊ![]() .
.
ЃЈЂђЃЉЫцЛњБфСП![]() ЕФЫљгаПЩФмЕФШЁжЕЮЊ0ЃЌ1,2.
ЕФЫљгаПЩФмЕФШЁжЕЮЊ0ЃЌ1,2.
![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]()
ЫљвдЃЌ ![]() ЕФЗжВМСаЮЊЃК
ЕФЗжВМСаЮЊЃК
| 0 | 1 | 2 |
|
|
|
|
![]()
![]()


 ЭЈГЧбЇЕфФЌаДФмЪжЯЕСаД№АИ
ЭЈГЧбЇЕфФЌаДФмЪжЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫНтФГаЃбЇЩњЕФЪгСІЧщПіЃЌЯжВЩгУЫцЛњГщбљЕФЗНЗЈДгИУаЃЕФ![]() СНАржаИїГщШЁ
СНАржаИїГщШЁ![]() УћбЇЩњНјааЪгСІМьВтЃЌМьВтЕФЪ§ОнШчЯТ:
УћбЇЩњНјааЪгСІМьВтЃЌМьВтЕФЪ§ОнШчЯТ:
![]() Ар
Ар![]() УћбЇЩњЕФЪгСІМьВтНсЙћЃК
УћбЇЩњЕФЪгСІМьВтНсЙћЃК ![]()
![]() Ар
Ар![]() УћбЇЩњЕФЪгСІМьВтНсЙћЃК
УћбЇЩњЕФЪгСІМьВтНсЙћЃК ![]()
ЃЈЂёЃЉЗжБ№МЦЫуСНзщЪ§ОнЕФЦНОљЪ§ЃЌДгМЦЫуНсЙћПДЃЌФФИіАрЕФбЇЩњЕФЪгСІНЯКУЃПВЂМЦЫу![]() АрЕФ
АрЕФ![]() УћбЇЩњЪгСІЕФЗНВюЃЛ
УћбЇЩњЪгСІЕФЗНВюЃЛ
ЃЈЂђЃЉЯжДг![]() АрЕФЩЯЪі
АрЕФЩЯЪі![]() УћбЇЩњжаЫцЛњбЁШЁ
УћбЇЩњжаЫцЛњбЁШЁ![]() УћЃЌЧѓет
УћЃЌЧѓет![]() УћбЇЩњжажСЩйга
УћбЇЩњжажСЩйга![]() УћбЇЩњЕФЪгСІЕЭгк
УћбЇЩњЕФЪгСІЕЭгк![]() ЕФИХТЪ.
ЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙЋдЊ![]() ФъзѓгвЃЌЮвЙњЪ§бЇМвСѕЛеЗЂЯжЕБдВФкНге§ЖрБпаЮЕФБпЪ§ЮоЯодіМгЪБЃЌЖрБпаЮЕФУцЛ§ПЩЮоЯоБЦНќдВЕФУцЛ§ЃЌВЂДДСЂСЫЁАИюдВЪѕЁБСѕЛеЕУЕНСЫдВжмТЪОЋШЗЕНаЁЪ§ЕуКѓСНЮЛЕФНќЫЦжЕ
ФъзѓгвЃЌЮвЙњЪ§бЇМвСѕЛеЗЂЯжЕБдВФкНге§ЖрБпаЮЕФБпЪ§ЮоЯодіМгЪБЃЌЖрБпаЮЕФУцЛ§ПЩЮоЯоБЦНќдВЕФУцЛ§ЃЌВЂДДСЂСЫЁАИюдВЪѕЁБСѕЛеЕУЕНСЫдВжмТЪОЋШЗЕНаЁЪ§ЕуКѓСНЮЛЕФНќЫЦжЕ![]() ЃЌетОЭЪЧжјУћЕФЁАЛеТЪЁБ.ШчЭМЪЧРћгУСѕЛеЕФЁАИюдВЪѕЁБЫМЯыЩшМЦЕФвЛИіГЬађПђЭМЃЌЦфжа
ЃЌетОЭЪЧжјУћЕФЁАЛеТЪЁБ.ШчЭМЪЧРћгУСѕЛеЕФЁАИюдВЪѕЁБЫМЯыЩшМЦЕФвЛИіГЬађПђЭМЃЌЦфжа![]() БэЪОдВФкНге§ЖрБпаЮЕФБпЪ§ЃЌжДааДЫЫуЗЈЪфГіЕФдВжмТЪЕФНќЫЦжЕвРДЮЮЊ ЃЈ ЃЉ
БэЪОдВФкНге§ЖрБпаЮЕФБпЪ§ЃЌжДааДЫЫуЗЈЪфГіЕФдВжмТЪЕФНќЫЦжЕвРДЮЮЊ ЃЈ ЃЉ
ЃЈВЮПМЪ§ОнЃК ![]() ЃЉ
ЃЉ
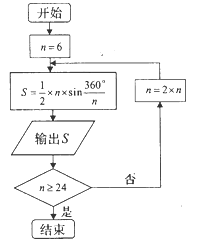
A. 2.598,3,3.1048 B. 2.598,3,3.1056
C. 2.578,3,3.1069 D. 2.588,3,3.1108
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=sinЃЈІиx+ІеЃЉЃЈІиЃО0ЃЌ|Іе|ЃМ ![]() ЃЉЕФзюаЁе§жмЦкЪЧІаЃЌШєЦфЭМЯѓЯђгвЦНвЦ
ЃЉЕФзюаЁе§жмЦкЪЧІаЃЌШєЦфЭМЯѓЯђгвЦНвЦ ![]() ИіЕЅЮЛКѓЕУЕНЕФКЏЪ§ЮЊЦцКЏЪ§ЃЌдђКЏЪ§y=fЃЈxЃЉЕФЭМЯѓЃЈ ЃЉ
ИіЕЅЮЛКѓЕУЕНЕФКЏЪ§ЮЊЦцКЏЪ§ЃЌдђКЏЪ§y=fЃЈxЃЉЕФЭМЯѓЃЈ ЃЉ
A.ЙигкЕуЃЈ ![]() ЃЌ0ЃЉЖдГЦ
ЃЌ0ЃЉЖдГЦ
B.ЙигкжБЯпx= ![]() ЖдГЦ
ЖдГЦ
C.ЙигкЕуЃЈ ![]() ЃЌ0ЃЉЖдГЦ
ЃЌ0ЃЉЖдГЦ
D.ЙигкжБЯпx= ![]() ЖдГЦ
ЖдГЦ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯп![]() ЕФНЙЕуЮЊ
ЕФНЙЕуЮЊ![]() ЃЌХзЮяЯпЩЯКсзјБъЮЊ
ЃЌХзЮяЯпЩЯКсзјБъЮЊ![]() ЕФЕуЕНХзЮяЯпЖЅЕуЕФОрРыгыИУЕуЕНХзЮяЯпзМЯпЕФОрРыЯрЕШЁЃ
ЕФЕуЕНХзЮяЯпЖЅЕуЕФОрРыгыИУЕуЕНХзЮяЯпзМЯпЕФОрРыЯрЕШЁЃ
ЃЈ1ЃЉЧѓХзЮяЯп![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉЩшжБЯп![]() гыХзЮяЯп
гыХзЮяЯп![]() НЛгк
НЛгк![]() СНЕуЃЌШє
СНЕуЃЌШє![]() ЃЌЧѓЪЕЪ§
ЃЌЧѓЪЕЪ§![]() ЕФжЕЁЃ
ЕФжЕЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПДгФГаЃЫцЛњГщШЁ100УћбЇЩњЃЌЛёЕУСЫЫћУЧвЛжмПЮЭтдФЖСЪБМфЃЈЕЅЮЛЃКаЁЪБЃЉЕФЪ§ОнЃЌећРэЕУЕНЪ§ОнЗжзщМАЦЕЪ§ЗжВМБэКЭЦЕТЪЗжВМжБЗНЭМЃК
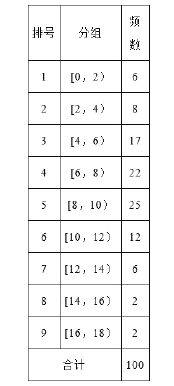
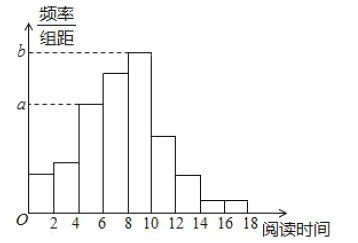
ЃЈЂёЃЉДгИУаЃЫцЛњбЁШЁвЛУћбЇЩњЃЌЪдЙРМЦетУћбЇЩњИУжмПЮЭтдФЖСЪБМфЩйгк12аЁЪБЕФИХТЪЃЛ
ЃЈЂђЃЉЧѓЦЕТЪЗжВМжБЗНЭМжаЕФ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈЂѓЃЉДгдФЖСЪБМфдк![]() ЕФбЇЩњжаШЮбЁ2ШЫЃЌЧѓЧЁКУга1ШЫдФЖСЪБМфдк
ЕФбЇЩњжаШЮбЁ2ШЫЃЌЧѓЧЁКУга1ШЫдФЖСЪБМфдк![]() ЃЌСэ1 ШЫдФЖСЪБМфдк
ЃЌСэ1 ШЫдФЖСЪБМфдк![]() ЕФИХТЪ.
ЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПГБжнЭГМЦОжОЭФГЕиОгУёЕФдТЪеШыЕїВщСЫ![]() ШЫЃЌВЂИљОнЫљЕУЪ§ОнЛСЫбљБОЕФЦЕТЪЗж
ШЫЃЌВЂИљОнЫљЕУЪ§ОнЛСЫбљБОЕФЦЕТЪЗж
ВМжБЗНЭМЃЈУПИіЗжзщАќРЈзѓЖЫЕуЃЌВЛАќРЈгвЖЫЕуЃЌШчЕквЛзщБэЪОЪеШыдк![]() ЃЉЁЃ
ЃЉЁЃ

ЃЈ1ЃЉЧѓОгУёдТЪеШыдк![]() ЕФЦЕТЪЃЛ
ЕФЦЕТЪЃЛ
ЃЈ2ЃЉИљОнЦЕТЪЗжВМжБЗНЭМЫуГібљБОЪ§ОнЕФжаЮЛЪ§ЃЛ
ЃЈ3ЃЉЮЊСЫЗжЮіОгУёЕФЪеШыгыФъСфЁЂжАвЕЕШЗНУцЕФЙиЯЕЃЌБиаыАДдТЪеШыдйДгет![]() ШЫжаЗжВуГщбљЗНЗЈГщГі
ШЫжаЗжВуГщбљЗНЗЈГщГі![]() ШЫзїНјвЛВНЗжЮіЃЌдђдТЪеШыдк
ШЫзїНјвЛВНЗжЮіЃЌдђдТЪеШыдк![]() ЕФетЖЮгІГщЖрЩйШЫЃП
ЕФетЖЮгІГщЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИјГі20ИіЪ§ЃЌ1ЃЌ2ЃЌ4ЃЌ7ЃЌ11ЃЌЁЃЌЦфЙцТЩЪЧЃКЕк1ИіЪ§ЪЧ1ЃЌЕк2ИіЪ§БШЕк1ИіЪ§Дѓ1ЃЌЕк3ИіЪ§БШЕк2ИіЪ§Дѓ2ЃЌЕк4ИіЪ§БШЕк3ИіЪ§Дѓ3ЃЌЁЃЌвдДЫРрЭЦЃЌШчЭМЫљЪОЕФГЬађПђЭМЕФЙІФмЪЧМЦЫует20ИіЪ§ЕФКЭ.


(1)ЧыдкГЬађПђЭМжаЬюаДСНИіЃЈ_______ЃЉФкШБЩйЕФФкШнЃЛ
(2)ЧыВЙГфЭъећИУГЬађПђЭМЖдгІЕФМЦЫуЛњГЬађ(гУWHILEгяОфБраД).
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЃЈ0ЃЌ2ІаЃЉФкЃЌЪЙsinxЉcosxЃМ0ГЩСЂЕФxШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
A.ЃЈ ![]() ЃЌ
ЃЌ ![]() ЃЉ
ЃЉ
B.ЃЈ0ЃЌ ![]() ЃЉ
ЃЉ
C.ЃЈ ![]() ЃЌІаЃЉЁШЃЈ
ЃЌІаЃЉЁШЃЈ ![]() ЃЌ2ІаЃЉ
ЃЌ2ІаЃЉ
D.ЃЈ0ЃЌ ![]() ЃЉЁШЃЈ
ЃЉЁШЃЈ ![]() ЃЌ2ІаЃЉ
ЃЌ2ІаЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com