
已知函数f(x)=ln x-ax+1在x=2处的切线斜率为- .
.
(1)求实数a的值及函数f(x)的单调区间;
(2)设g(x)= ,对?x1∈(0,+∞),?x2∈(-∞,0)使得f(x1)≤g(x2)成立,求正实数k的取值范围;
,对?x1∈(0,+∞),?x2∈(-∞,0)使得f(x1)≤g(x2)成立,求正实数k的取值范围;
(3)证明: +
+ +…+
+…+ <
< (n∈N*,n≥2).
(n∈N*,n≥2).
(1)即f(x)的单调递增区间为(0,1),单调递减区间为(1,+∞).
(2)k≥1
(3)见解析
【解析】(1)解 由已知得f′(x)= -a,∴f′(2)=
-a,∴f′(2)= -a=-
-a=- ,解得a=1.
,解得a=1.
于是f′(x)= -1=
-1= ,
,
当x∈(0,1)时,f′(x)>0,f(x)为增函数,
当x∈(1,+∞)时,f′(x)<0,f(x)为减函数,
即f(x)的单调递增区间为(0,1),单调递减区间为(1,+∞).
(2)解 由(1)知x1∈(0,+∞),f(x1)≤f(1)=0,即f(x1)的最大值为0,
由题意知:对?x1∈(0,+∞),?x2∈(-∞,0)使得f(x1)≤g(x2)成立,
只需f(x)max≤g(x)max.
∵g(x)= =x+
=x+ +2k=-
+2k=- +2k≤-2
+2k≤-2 +2k,
+2k,
∴只需-2 +2k≥0,解得k≥1.
+2k≥0,解得k≥1.
(3)证明 要证明 +
+ +…+
+…+ <
< (n∈N*,n≥2).
(n∈N*,n≥2).
只需证 +
+ +…+
+…+ <
< ,
,
只需证 +
+ +…+
+…+ <
< .
.
由(1)当x∈(1,+∞)时,f′(x)<0,f(x)为减函数,
f(x)=ln x-x+1≤0,即ln x≤x-1,
∴当n≥2时,ln n2<n2-1,
 <
< =1-
=1- <1-
<1- =1-
=1- +
+ ,
,
 +
+ +…+
+…+ <
< +
+ +…+
+…+ =n-1-
=n-1- +
+ =
= ,
,
∴ +
+ +…+
+…+ <
< .
.


科目:高中数学 来源:2014高考名师推荐数学文科函数的定义域、值域(解析版) 题型:选择题
已知函数f(x)的定义域为(-1,0),则函数f(2x+1)的定义域为( )
A. (-1, 1)
B. 
C. (-1,0)
D. 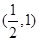
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科y=Asinwx+图像(解析版) 题型:选择题
为了得到函数 的图象,只需把函数
的图象,只需把函数 的图象( )
的图象( )
A. 向左平移 个单位长度
个单位长度
B. 向右平移 个单位长度
个单位长度
C. 向左平移 个单位长度
个单位长度
D. 向右平移 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(四)(解析版) 题型:解答题
如图,已知平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.

(1)求证:GH∥平面CDE;
(2)若CD=2,DB=4 ,求四棱锥F—ABCD的体积.
,求四棱锥F—ABCD的体积.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(四)(解析版) 题型:选择题
在△ABC中,内角A,B,C的对边分别是a,b,c,若cos B= ,
, =2,且S△ABC=
=2,且S△ABC= , 则b的值为( )
, 则b的值为( )
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(二)(解析版) 题型:解答题
设函数f(x)=ax2+(b-2)x+3(a≠0),若不等式f(x)>0的解集为(-1,3).
(1)求a,b的值;
(2)若函数f(x)在x∈[m,1]上的最小值为1,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com