
如图,已知平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.

(1)求证:GH∥平面CDE;
(2)若CD=2,DB=4 ,求四棱锥F—ABCD的体积.
,求四棱锥F—ABCD的体积.
(1)见解析 (2)16
【解析】(1)证明 方法一 ∵EF∥AD,AD∥BC,∴EF∥BC.
又EF=AD=BC,∴四边形EFBC是平行四边形,
∴H为FC的中点.
又∵G是FD的中点,∴HG∥CD.
∵HG?平面CDE,CD?平面CDE,
∴GH∥平面CDE.

方法二 连接EA,∵ADEF是正方形,
∴G是AE的中点.
∴在△EAB中,GH∥AB.
又∵AB∥CD,∴GH∥CD.
∵HG?平面CDE,CD?平面CDE,
∴GH∥平面CDE.
(2)解 ∵平面ADEF⊥平面ABCD,交线为AD,
且FA⊥AD,∴FA⊥平面ABCD.
∵AD=BC=6,∴FA=AD=6.
又∵CD=2,DB=4 ,CD2+DB2=BC2,∴BD⊥CD.
,CD2+DB2=BC2,∴BD⊥CD.
∵S?ABCD=CD·BD=8 ,
,
∴VF—ABCD= S?ABCD·FA=
S?ABCD·FA= ×8
×8 ×6=16
×6=16 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(四)(解析版) 题型:解答题
已知函数f(x)=ln x-ax+1在x=2处的切线斜率为- .
.
(1)求实数a的值及函数f(x)的单调区间;
(2)设g(x)= ,对?x1∈(0,+∞),?x2∈(-∞,0)使得f(x1)≤g(x2)成立,求正实数k的取值范围;
,对?x1∈(0,+∞),?x2∈(-∞,0)使得f(x1)≤g(x2)成立,求正实数k的取值范围;
(3)证明: +
+ +…+
+…+ <
< (n∈N*,n≥2).
(n∈N*,n≥2).
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(四)(解析版) 题型:选择题
已知定义域为R的函数f(x)满足:f(4)=-3,且对任意x∈R总有f′(x)<3,则不等式f(x)<3x-15的解集为( )
A.(-∞,4)
B.(-∞,-4)
C.(-∞,-4)∪(4,+∞)
D.(4,+∞)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(四)(解析版) 题型:选择题
已知α,β表示两个不同的平面,m是一条直线且m?α,则:“α⊥β”是“m⊥β”的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(二)(解析版) 题型:选择题
给出下列四个命题,其中不正确的命题为( )
①若cos α=cos β,则α-β=2kπ,k∈Z;
②函数y=2cos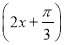 的图象关于x=
的图象关于x=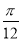 对称;
对称;
③函数y=cos(sin x)(x∈R)为偶函数;
④函数y=sin|x|是周期函数,且周期为2π.
A.①② B.①④ C.①②③ D.①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com