
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 设等差数列{an}的公差为d,d≠0.可得:Sn=na1+$\frac{n(n-1)}{2}$d=$\frac{d}{2}$$(n-\frac{d-2{a}_{1}}{2d})^{2}$-$\frac{(d-2{a}_{1})^{2}}{8d}$,数列{Sn}单调递增,可得d>0,$\frac{d-2{a}_{1}}{2d}$≤1,因此d+2a1≥0.由a2>0且a1>0,可得a2=a1+d>0.即可判断出结论.
解答 解:设等差数列{an}的公差为d,d≠0.
Sn=na1+$\frac{n(n-1)}{2}$d
=$\frac{d}{2}$n2+$({a}_{1}-\frac{d}{2})n$
=$\frac{d}{2}$$(n-\frac{d-2{a}_{1}}{2d})^{2}$-$\frac{(d-2{a}_{1})^{2}}{8d}$,
∵数列{Sn}单调递增,
∴d>0,$\frac{d-2{a}_{1}}{2d}$≤1,
可得d+2a1≥0.
由a2>0且a1>0,可得a2=a1+d>0.
∴“a2>0且a1>0”是“数列{Sn}单调递增”的既不充分又不必要条件.
故选:D.
点评 本题考查了函数的性质、不等式的性质、等差数列的通项公式及其前n项和公式、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
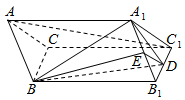 如图,在三棱柱ABC-A1B1C1中,A1B1=A1C1,点D,E分别是B1C1,A1B1的中点,AA1=AB=BD=1,∠A1AB=60°.
如图,在三棱柱ABC-A1B1C1中,A1B1=A1C1,点D,E分别是B1C1,A1B1的中点,AA1=AB=BD=1,∠A1AB=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 20 | C. | 8 | D. | 24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com