
| A. | y=cosx | B. | y=cos2x | C. | y=sin2x | D. | y=-tan2x |
分析 根据三角函数周期的计算公式,正余弦函数的单调性及单调性的定义即可判断每个选项的正误,从而找出正确选项.
解答 解:A.y=cosx的周期为2π,∴该选项错误;
B.y=cos2x的周期为π;
∵$x∈[0,\frac{π}{2}]$;
∴2x∈[0,π],且y=cosx在[0,π]上为减函数;
∴y=cos2x在$[0,\frac{π}{2}]$上是减函数;
∴该选项正确;
C.2x∈[0,π],且y=sinx在[0,π]上没有单调性;
∴y=sin2x在$[0,\frac{π}{2}]$上没有单调性,∴该选项错误;
D.2x∈[0,π],且y=-tanx在[0,π]上没有单调性,∴该选项错误.
故选B.
点评 考查形如y=Asin(ωx+φ)的周期的计算公式,以及正余弦函数的单调性,函数单调性定义,不等式的性质.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,5] | B. | (-∞,4] | C. | (-∞,2] | D. | (-∞,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B,C两点,弦CD∥AP,AD,BC相交于点E,F为CE上一点,且DE2=EF•EC.
如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B,C两点,弦CD∥AP,AD,BC相交于点E,F为CE上一点,且DE2=EF•EC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}x=2x'\\ y=3y'\end{array}\right.$ | B. | .$\left\{\begin{array}{l}x=\frac{1}{2}x'\\ y=\frac{1}{3}y'\end{array}\right.$ | C. | .$\left\{\begin{array}{l}x=4x'\\ y=9y'\end{array}\right.$ | D. | .$\left\{\begin{array}{l}x=\frac{1}{4}x'\\ y=\frac{1}{9}y'\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
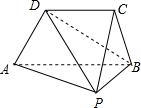 如图,四棱锥P-ABCD,DC∥AB,PB⊥AB,平面PAB⊥平面ABCD,AD=DC=CB=1,AB=BP=2
如图,四棱锥P-ABCD,DC∥AB,PB⊥AB,平面PAB⊥平面ABCD,AD=DC=CB=1,AB=BP=2查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com