练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】选修4-4：坐标系与参数方程

    在平面直角坐标系中，直线的参数方程为（为参数），以原点为极点， 轴的正半轴为极轴，取相同的长度单位建立极坐标系，圆的极坐标方程为.

    （1）求圆的直角坐标方程，并写出圆心和半径；

    （2）若直线与圆交于两点，求的最大值和最小值.

    【答案】(1)见解析;(2) 的最大值为，最小值为.

    【解析】试题分析：（1）根据，把直线的极坐标方程转化为直角坐标方程，进而得到圆心和半径；（2）把直线的参数方程代入圆的标准方程，得，利用根与系数的关系表示，从而得到最值.

    试题解析：

    （1）

    ,

    .

    圆心为，半径为.

    （2）把直线的参数方程代入圆的标准方程，

    得，

    整理得，

    ，

    设两点对应的参数分别为，

    则， .

    所以

    ,

    .

    因为，

    所以，

    即的最大值为，最小值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设数列的前项和为，若（），则称是“紧密数列”.

    （1）已知数列是“紧密数列”，其前5项依次为，求的取值范围；

    （2）若数列的前项和为（），判断是否是“紧密数列”，并说明理由；

    （3）设是公比为的等比数列，若与都是“紧密数列”，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知△ABC的内角A，B，C的对边分别为a，b，c.且满足4cos2cos2（B+C）.

    （1）求角A；

    （2）若△ABC的面积为，周长为8，求a.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我国华南沿海地区是台风登陆频繁的地区，为统计地形地貌对台风的不同影响，把华南沿海分成东西两区，对台风的强度按风速划分为：风速不小于30米/秒的称为强台风，风速小于30米/秒的称为风暴，下表是2014年对登陆华南地区的15次台风在东西两部的强度统计：

    （1）根据上表，计算有没有99%以上的把握认为台风强度与东西地域有关；

    （2）2017年8月23日，“天鸽”在深圳登陆，造成深圳特大风暴，如图所示的茎叶图统计了深圳15块区域的风速.（十位数为茎，个位数为叶）

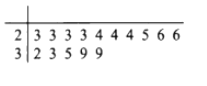
    ①任取2个区域进行统计，求取到2个区域风速不都小于25的概率；

    ②任取3个区域进行统计， 表示“风速达到强台风级别的区域个数”，求的分布列及数学期望.

    附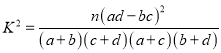： ，其中.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥，底面是边长为2的菱形， ，且平面.

    （1）证明：平面平面；

    （2）若平面与平面的夹角为，试求线段的长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （Ⅰ）讨论函数的单调性；

    （Ⅱ）若函数有极小值，求该极小值的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某医院为促进行风建设，拟对医院的服务质量进行量化考核，每个患者就医后可以对医院进行打分，最高分为100分.上个月该医院对100名患者进行了回访调查，将他们按所打分数分成以下几组：第一组，第二组，第三组，第四组，第五组，得到频率分布直方图，如图所示.

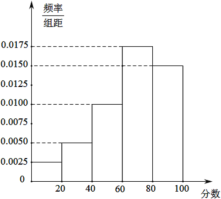
    （1）求所打分数不低于60分的患者人数；

    （2）该医院在第二三组患者中按分层抽样的方法抽取6名患者进行深入调查，之后将从这6人中随机抽取2人聘为医院行风监督员，求行风监督员来自不同组的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数定义域为R，对于任意R恒有.

    （1）若，求的值；

    （2）若时，，求函数，的解析式及值域；

    （3）若时，，求在区间，上的最大值与最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

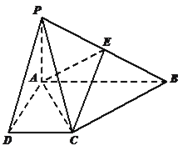
    【题目】如图，在四棱锥中， 底面， ， ∥， ， ．

    （1）求证：平面 平面;

    （2）若棱上存在一点，使得二面角的余弦值为，求与平面所成角的正弦值．

    查看答案和解析>>

    同步练习册答案