
分析 (1)根据单调性依据闭区间的定义等价转化为方程,直接求解;
(2)根据闭函数的定义一定存在区间[a,b],由定义直接转化:a,b为方程x=k+$\sqrt{x+2}$的两个实数根,
即方程x2-(2k+1)x+k2-2=0(x≥-2,x≥k)有两个不等的实根,由二次方程实根分布求解即可.
解答 解:(1)由题意,y=-x3在[a,b]上递减,
则$\left\{\begin{array}{l}{b=-{a}^{3}}\\{a=-{b}^{3}}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-1}\\{b=1}\end{array}\right.$,
所以,所求的区间为[-1,1];
(2)若函数$y=k+\sqrt{x+2}$是闭函数,且为[-2,+∞)的增函数,则存在区间[a,b],
在区间[a,b]上,函数f(x)的值域为[a,b],
即$\left\{\begin{array}{l}{a=k+\sqrt{a+2}}\\{b=k+\sqrt{b+2}}\end{array}\right.$,
可得a,b为方程x=k+$\sqrt{x+2}$的两个实数根,
即方程x2-(2k+1)x+k2-2=0(x≥-2,x≥k)有两个不等的实根,
设f(x)=x2-(2k+1)x+k2-2,
当k≤-2时,有$\left\{\begin{array}{l}{△=(2k+1)^{2}-4({k}^{2}-2)>0}\\{f(-2)={k}^{2}+4k+4≥0}\\{\frac{2k+1}{2}>-2}\end{array}\right.$,即为$\left\{\begin{array}{l}{k>-\frac{9}{4}}\\{k∈R}\\{k>-\frac{5}{2}}\end{array}\right.$,解得-$\frac{9}{4}$<k≤-2,
当k>-2时,有$\left\{\begin{array}{l}{△=(2k+1)^{2}-4({k}^{2}-2)>0}\\{f(k)=-k-2≥0}\\{\frac{2k+1}{2}>k}\end{array}\right.$,即有$\left\{\begin{array}{l}{k>-\frac{9}{4}}\\{k≤-2}\\{k∈R}\end{array}\right.$,无解,
综上所述,k的取值范围是(-$\frac{9}{4}$,-2].
点评 本题考查函数的单调性及新定义型函数的理解,以及问题的等价转化能力,运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
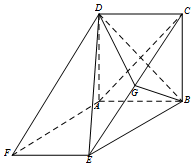 如图,ABCD是边长为3的正方形,ABEF是矩形,平面ABCD⊥平面ABEF,G为EC的中点.
如图,ABCD是边长为3的正方形,ABEF是矩形,平面ABCD⊥平面ABEF,G为EC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
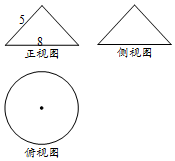 若某几何体的三视图如图所示,其中正视图与侧视图是两个全等的等腰三角形,则此几何体的表面积是( )
若某几何体的三视图如图所示,其中正视图与侧视图是两个全等的等腰三角形,则此几何体的表面积是( )| A. | 36π | B. | 30π | C. | 24π | D. | 15π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,+∞) | B. | (0,+∞) | C. | (1,+∞) | D. | (4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
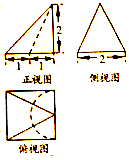 某零件的三视图如图所示,则该零件的体积为( )
某零件的三视图如图所示,则该零件的体积为( )| A. | $\frac{7}{3}$ | B. | $\frac{8-π}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{7-π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com