
袋中有红、黄、白三种颜色的球各一个,从中每次取一只,有放回的抽取三次,
求:(1)3只球颜色全相同的概率;
(2)3只球颜色不全相同的概率;
(3)3只球颜色全不相同的概率.
科目:高中数学 来源: 题型:解答题
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是: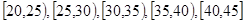 .
.
(I)求图中 的值并根据频率分布直方图估计这500名志愿者中年龄在
的值并根据频率分布直方图估计这500名志愿者中年龄在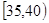 岁的人数;
岁的人数;
(II)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加中心广场的宣传活动,再从这20名中采用简单随机抽样方法选取3名志愿者担任主要负责人.记这3名志愿者中“年龄低于35岁”的人数为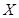 ,求
,求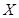 的分布列及数学期望.
的分布列及数学期望. 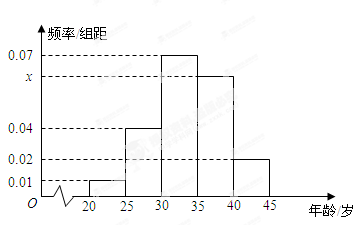
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两支排球队进行比赛,约定先胜 局者获得比赛的胜利,比赛随即结束。除第五局甲队获胜的概率是
局者获得比赛的胜利,比赛随即结束。除第五局甲队获胜的概率是 外,其余每局比赛甲队获胜的概率都是
外,其余每局比赛甲队获胜的概率都是 。假设各局比赛结果相互独立。
。假设各局比赛结果相互独立。
(Ⅰ)分别求甲队以 胜利的概率;
胜利的概率;
(Ⅱ)若比赛结果为求 或
或 ,则胜利方得
,则胜利方得 分,对方得
分,对方得 分;若比赛结果为
分;若比赛结果为 ,则胜利方得
,则胜利方得 分、对方得
分、对方得 分。求乙队得分
分。求乙队得分 的分布列及数学期望。
的分布列及数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
2013年3月2日,国家环保部发布了新修订的《环境空气质量标准》.其中规定:居民区的PM2.5年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米. 某城市环保部门随机抽取了一居民区去年20天PM2.5的24小时平均浓度的监测数据,数据统计如下:
| 组别 | PM2.5浓度 (微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,25] | 5 | 0.25 |
| 第二组 | (25,50] | 10 | 0.5 |
| 第三组 | (50,75] | 3 | 0.15 |
| 第四组 | (75,100) | 2 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.
| 一次购物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
| 顾客数(人) |  | 30 | 25 |  | 10 |
| 结算时间(分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
2012年3月2日,国家环保部发布了新修订的《环境空气质量标准》。其中规定:居民区的PM2.5(大气中直径小于或等于2.5微米的颗粒物)年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米。某城市环保部门随机抽取了一居民区去年20天PM2.5的24小时平均浓度的监测数据,数据统计如下:
| 组别 | PM2.5浓度 (微克/立方米 | 频数(天) | 频率 |
| 第一组 | (0,25] | 5 | 0.25 |
| 第二组 | (25,50] | 10 | 0.5 |
| 第三组 | (50,75] | 3 | 0.15 |
| 第四组 | (75,100) | 2 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某学校篮球队、羽毛球队、乒乓球队的某些队员不止参加了一支球队,具体情况如图所示,现从中随机抽取一名队员,求:
(1)该队员只属于一支球队的概率;
(2)该队员最多属于两支球队的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
四名教师被分到甲、乙、丙三所学校参加工作,每所学校至少一名教师.
(Ⅰ)求 、
、 两名教师被同时分配到甲学校的概率;
两名教师被同时分配到甲学校的概率;
(Ⅱ)求 、
、 两名教师不在同一学校的概率;
两名教师不在同一学校的概率;
(Ⅲ)设随机变量 为这四名教师中分配到甲学校的人数,求
为这四名教师中分配到甲学校的人数,求 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市为了推动全民健身运动在全市的广泛开展,该市电视台开办了健身竞技类栏目《健身大闯关》,规定参赛者单人闯关,参赛者之间相互没有影响,通过关卡者即可获奖。现有甲、乙、丙 人参加当天的闯关比赛,已知甲获奖的概率为
人参加当天的闯关比赛,已知甲获奖的概率为 ,乙获奖的概率为
,乙获奖的概率为 ,丙获奖而甲没有获奖的概率为
,丙获奖而甲没有获奖的概率为 。
。
(Ⅰ)求三人中恰有一人获奖的概率;
(Ⅱ)求三人中至少有两人获奖的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com