
【题目】已知抛物线![]() 的焦点为F,直线
的焦点为F,直线![]() 与x轴的交点为P,与抛物线的交点为Q,且
与x轴的交点为P,与抛物线的交点为Q,且![]() .
.

![]() 求抛物线的方程;
求抛物线的方程;
![]() 如图所示,过F的直线l与抛物线相交于
如图所示,过F的直线l与抛物线相交于![]() 两点,与圆
两点,与圆![]() 相交于
相交于![]() 两点
两点![]() 两点相邻
两点相邻![]() ,过
,过![]() 两点分别作抛物线的切线,两条切线相交于点M,求
两点分别作抛物线的切线,两条切线相交于点M,求![]() 与
与![]() 的面积之积的最小值.
的面积之积的最小值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,P是⊙O外一点,PA是切线,A为切点,割线PBC与⊙O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交⊙O于点E,证明: 
(1)BE=EC;
(2)ADDE=2PB2 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某连锁经营公司所属5个零售店某月的销售额和利润额资料如表所示:
商店名称 | A | B | C | D | E |
销售额(x)/千万元 | 3 | 5 | 6 | 7 | 9 |
利润额(y)/百万元 | 2 | 3 | 3 | 4 | 5 |
(1)画出销售额和利润额的散点图.
(2)若销售额和利润额具有相关关系,用最小二乘法计算利润额y对销售额x的回归直线方程![]() =
=![]() x+
x+![]() ,其中
,其中![]() =
=![]() ,
,![]() =
=![]() -
-![]()
![]() .
.
(3)若获得利润是4.5百万元时估计销售额是多少(千万元)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图显示. 
(1)已知[30,40)、[40,50)、[50,60)三个年龄段的上网购物者人数成等差数列,求a,b的值.
(2)该电子商务平台将年龄在[30,50)之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放100元的代金券,现采用分层抽样的方式从参与调查的1000位上网购者中抽取10人,并在这10人中随机抽取3人进行回访,求此三人获得代金券总和X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以坐标原点为极点, ![]() 轴的非负半轴为极轴建立极坐标系,已知曲线
轴的非负半轴为极轴建立极坐标系,已知曲线![]() :
:![]() ,点
,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,且点
,且点![]() 在直线
在直线![]() 上.
上.
(1)求曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 向左平移
向左平移![]() 个单位长度后得到
个单位长度后得到![]() ,
,![]() 到
到![]() 的交点为
的交点为![]() ,
, ![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD是菱 形,PA=PB,且侧面PAB⊥平面ABCD,点E是AB的中点.
中,底面ABCD是菱 形,PA=PB,且侧面PAB⊥平面ABCD,点E是AB的中点.
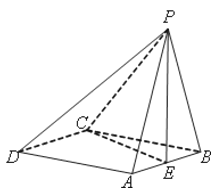
(1)求证:PE⊥AD;
(2)若CA=CB,求证:平面PEC⊥平面PAB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市拟定2016年城市建设A,B,C三项重点工程,该市一大型城建公司准备参加这三个工程的竞标,假设这三个工程竞标成功与否相互独立,该公司对A,B,C三项重点工程竞标成功的概率分别为a,b, ![]() (a>b),已知三项工程都竞标成功的概率为
(a>b),已知三项工程都竞标成功的概率为 ![]() ,至少有一项工程竞标成功的概率为
,至少有一项工程竞标成功的概率为 ![]() .
.
(1)求a与b的值;
(2)公司准备对该公司参加A,B,C三个项目的竞标团队进行奖励,A项目竞标成功奖励2万元,B项目竞标成功奖励4万元,C项目竞标成功奖励6万元,求竞标团队获得奖励金额的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com