
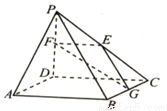
(本小题满分12分)如图,在四棱锥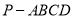 中,
中,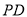
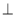 底面
底面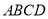 ,且底面
,且底面 为正方形,
为正方形, 分别为
分别为 的中点.
的中点.
(1)求证: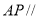 平面
平面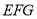 ;
;
(2)求平面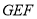 和平面
和平面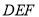 的夹角.
的夹角.
证明见解析
【解析】
试题分析::(1)利用已知的线面垂直关系建立空间直角坐标系,准确写出相关点的坐标,从而将几何证明转化为向量运算.其中灵活建系是解题的关键.(2)证明线面平行,需证线线平行,只需要证明直线的方向向量与平面的法向量垂直;(3)把向量夹角的余弦值转化为两平面法向量夹角的余弦值;(4)空间向量将空间位置关系转化为向量运算,应用的核心是要充分认识形体特征,建立恰当的坐标系,实施几何问题代数化.同时注意两点:一是正确写出点、向量的坐标,准确运算;二是空间位置关系中判定定理与性质定理条件要完备.
试题解析:(1)如图,以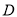 为原点,以
为原点,以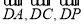 为方向向量
为方向向量
建立空间直角坐标系
则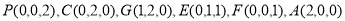 .
.
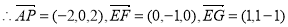 .
.
设平面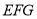 的法向量为
的法向量为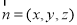
 即
即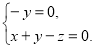
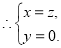 令
令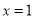
则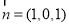 .
.

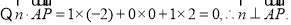
又 平面
平面 平面
平面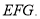
(2)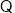 底面
底面 是正方形,
是正方形,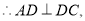 又
又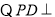 平面
平面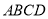
 又
又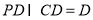 ,
,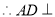 平面
平面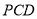
 向量
向量 是平面
是平面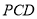 的一个法向量,
的一个法向量,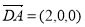 又由(1)知平面
又由(1)知平面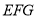 的法向量
的法向量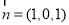 .
.

 二面角
二面角 的平面角为
的平面角为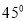 .
.
考点:(1)证明直线与平面平行;(2)利用空间向量解决二面角问题.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源:2015届陕西省西安市高二上学期期中考试数学试卷(解析版) 题型:选择题
在数列1,1,2,3,5,8,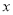 ,21,34,55中,
,21,34,55中,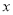 等于( )
等于( )
A.11 B.12 C.13 D.14
查看答案和解析>>
科目:高中数学 来源:2015届陕西南郑中学高二下学期期末考试理科数学试卷(解析版) 题型:填空题
如图所示,在一个边长为1的正方形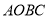 内,曲线
内,曲线 和曲线
和曲线 围成一个叶形图(阴影部分),向正方形
围成一个叶形图(阴影部分),向正方形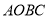 内随机投一点(该点落在正方形
内随机投一点(该点落在正方形 内任何一点是等可能的),则所投的点落在叶形图内部的概率是 .
内任何一点是等可能的),则所投的点落在叶形图内部的概率是 .

查看答案和解析>>
科目:高中数学 来源:2015届陕西南郑中学高二下学期期末考试理科数学试卷(解析版) 题型:选择题
已知双曲线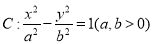 的左、右焦点分别为
的左、右焦点分别为
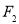 ,过
,过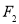 作双曲线
作双曲线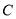 的一条渐近线的垂线,垂足为
的一条渐近线的垂线,垂足为 ,若
,若 的中点
的中点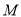 在双曲线
在双曲线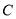 上,则双曲线
上,则双曲线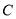 的离心率为( )
的离心率为( )
A. B.
B.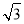 C.2 D.3
C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2016届辽宁省鞍山市高一下学期期末考试数学试卷(解析版) 题型:解答题
为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下:
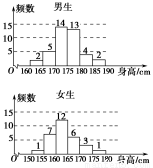
(1)估计该校学生身高在170~185 cm之间的概率;
(2)从样本中身高在180~190 cm之间的男生中任选2人,求至少有1人身高在185~190 cm之间的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com