
分析 由sin2A=sin2B,得2A=2B或2A+2B=π,从而判断三角形的形状判断①;利用“拆角配角”思想求值判断②;由函数图象的平移求出平移后的函数解析式判断③;
由已知求出tan2x判断④.
解答 解:①在△ABC中,若sin2A=sin2B,则2A=2B或2A+2B=π,即A=B或A+B=$\frac{π}{2}$,△ABC是等腰或直角三角形,故①错误;
②已知α是锐角,则$α+\frac{π}{4}∈$($\frac{π}{4},\frac{3π}{4}$),又$cos(α+\frac{π}{4})=\frac{3}{5}$,∴sin($α+\frac{π}{4}$)=$\frac{4}{5}$,
则$sinα=sin[(α+\frac{π}{4})-\frac{π}{4}]=sin(α+\frac{π}{4})cos\frac{π}{4}-cos(α+\frac{π}{4})sin\frac{π}{4}$=$\frac{4}{5}×\frac{\sqrt{2}}{2}-\frac{3}{5}×\frac{\sqrt{2}}{2}=\frac{\sqrt{2}}{10}$,故②正确;
③将函数$y=sin(2x+\frac{π}{3})$图象上的所有点向左平移$\frac{π}{12}$个单位,则得到的函数图象的解析式为$y=sin[2(x+\frac{π}{12})+\frac{π}{3}]=sin(2x+\frac{π}{2})=cos2x$,关于y对称,故③正确;
④由$sinx=-\frac{4}{5}$,$x∈(-\frac{π}{2},0)$,的cosx=$\frac{3}{5}$,∴tanx=$-\frac{4}{3}$,则tan2x=$\frac{2tanx}{1-ta{n}^{2}x}=\frac{-\frac{8}{3}}{1-\frac{16}{9}}=\frac{24}{7}$,故④正确.
∴正确命题的序号是②③④.
故答案为:②③④.
点评 本题考查命题的真假判定与应用,考查了三角函数的图象和性质,考查三角函数值的求法,是中档题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-2y+5=0 | B. | 2x-y+5=0 | C. | x+2y+5=0 | D. | 2x+y+5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1] | B. | (-∞,1)∪(4,+∞) | C. | (0,1)∪(4,+∞) | D. | (0,1]∪[4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{1}{2}$ | C. | $\frac{17}{24}$ | D. | -$\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
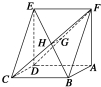 如图,已知平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
如图,已知平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com