Question

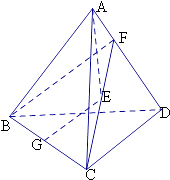
【题目】各棱长都等于4的四面ABCD中，设G为BC的中点，E为△ACD内的动点（含边界），且GE∥平面ABD，若 =1，则| |= ．

Answer 1

【答案】
【解析】解：连接CE，并延长交AD于F，连接BF，
由EG∥平面ABD，EG平面BCF，平面BCF∩平面ABD=BF，
可得EG∥BF，由G为BC的中点，可得E为CF的中点，
设AF=t，则 = （ + ）= （ + ），
在四面体ABCD中， = = =4×4× =8，
= （ + ）（ ﹣ ）
= （ ﹣ + 2﹣ ）
= （8﹣8+ 16﹣ 8）=1，
解得t=1，即 = （ + ），
可得| |2= （ 2+ 2+ ）
= ×（16+ ×16+ ×8）= ，
可得| |= ．
故答案为： ．

连接CE，并延长交AD于F，连接BF，运用线面平行的性质定理可得EG∥BF，由G为BC的中点，可得E为CF的中点，设AF=t，再由向量的中点的向量表示，结合向量的数量积的性质，解得t=1，再由向量的模的公式，计算即可得到所求值．