
【题目】已知椭圆![]() :
:![]()
![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,在
两点,在![]() 轴上存在点
轴上存在点![]() 满足
满足![]() ,求
,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)5
;(2)5
【解析】试题分析:
(Ⅰ)由椭圆的离心率为![]() 可得
可得![]() ,由椭圆过点
,由椭圆过点![]() ,故
,故![]() ,解得
,解得![]() ,
,![]() ,从而可得椭圆的方程.(Ⅱ)由题意可得
,从而可得椭圆的方程.(Ⅱ)由题意可得![]() 是线段
是线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交点,设直线的
轴交点,设直线的![]() 的方程为
的方程为![]() ,与椭圆的方程联立消元后根据所得的二次方程可得弦
,与椭圆的方程联立消元后根据所得的二次方程可得弦![]() 的中点
的中点![]() ,由此可得线段
,由此可得线段![]() 的垂直平分线的方程,进而得到点
的垂直平分线的方程,进而得到点![]() 再求得
再求得![]() 及三角形的高
及三角形的高![]() 后可得三角形的面积,根据基本不等式求得
后可得三角形的面积,根据基本不等式求得![]() 面积的最大值为5.
面积的最大值为5.
试题解析:
(Ⅰ)由题意得![]() ,
,
所以![]() .①
.①
因为点![]() 在椭圆
在椭圆![]() 上,
上,
所以![]() .②
.②
由①②得![]() ,
,![]() .
.
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)因为![]() 轴上存在点
轴上存在点![]() 满足
满足![]() ,
,
所以![]() 是线段
是线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交点.
轴交点.
由题意设直线的![]() 的方程为
的方程为![]() ,
,
由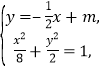 消去y整理得
消去y整理得![]() .
.
因为直线![]() 与椭圆交于两点,
与椭圆交于两点,
所以![]() ,
,
解得![]() .
.
设![]() ,
,![]() ,
,![]() 的中点为
的中点为![]() .
.
则![]() ,
,![]() .
.
所以![]() ,
,
故![]() ,
,
所以点![]() .
.
故线段![]() 的垂直平分线的方程为
的垂直平分线的方程为![]() ,即
,即![]() .
.
令![]() ,得
,得![]() ,即
,即![]() .
.
所以![]() ,即
,即![]() 的高
的高![]() ,
,
又![]()
![]()
![]()
![]() .
.
所以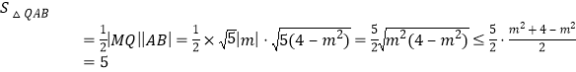 ,
,
当且仅当![]() ,即
,即![]() 时等号成立.
时等号成立.
验证可得![]() 满足
满足![]() .
.
所以![]() 面积的最大值为5.
面积的最大值为5.


科目:高中数学 来源: 题型:
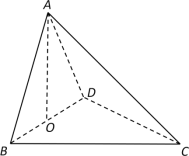
【题目】如图,将边长为2,有一个锐角为60°的菱形ABCD,沿着较短的对角线BD对折,使得![]() ,O为BD的中点.
,O为BD的中点.
(Ⅰ)求证:![]()
(Ⅱ)求三棱锥![]() 的体积;
的体积;
(Ⅲ)求二面角A-BC-D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设平面内到点![]() 和直线
和直线![]() 的距离相等的点的轨迹为曲线
的距离相等的点的轨迹为曲线![]() ,则曲线
,则曲线![]() 的方程为_______;若直线
的方程为_______;若直线![]() 与曲线
与曲线![]() 相交于不同两点
相交于不同两点![]() ,
, ![]() ,与圆
,与圆![]() 相切于点
相切于点![]() ,且
,且![]() 为线段
为线段![]() 的中点.在
的中点.在![]() 的变化过程中,满足条件的直线
的变化过程中,满足条件的直线![]() 有
有![]() 条,则
条,则![]() 的所有可能值为____________.
的所有可能值为____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内圆心为![]() 的圆的方程为
的圆的方程为![]() ,点
,点![]() 是圆上的动点,点
是圆上的动点,点![]() 是平面内任意一点,若线段
是平面内任意一点,若线段![]() 的垂直平分线交直线
的垂直平分线交直线![]() 于点
于点![]() ,则点
,则点![]() 的轨迹可能是_________.(请将下列符合条件的序号都填入横线上)
的轨迹可能是_________.(请将下列符合条件的序号都填入横线上)
①椭圆;②双曲线;③抛物线;④圆;⑤直线;⑥一个点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司的管理者通过公司近年来科研费用支出x(百万元)与公司所获得利润y(百万元)的散点图发现,y与x之间具有线性相关关系,具体数据如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
科研费用x(百万元) | 1.6 | 1.7 | 1.8 | 1.9 | 2.0 |
公司所获利润y(百万元) | 1 | 1.5 | 2 | 2.5 | 3 |
(1)求y关于x的回归直线方程;
(2)若该公司的科研投入从2011年开始连续10年每一年都比上一年增加10万元,预测2017年该公司可获得的利润约为多少万元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com