Question

16．已知棱长为$\sqrt{2}$的正方体的俯视图是一个面积为2的正方形，则该正方体的正视图的面积不可能等于（　　）

• A． $\sqrt{2}-1$
• B． 2
• C． $\sqrt{2}+1$
• D． $2\sqrt{2}$

Answer 1

分析 根据题意，画出图形，求出该正方体的正视图面积的取值范围，定义ABCD选项判断即可．

解答 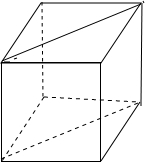解：根据题意，得；
水平放置的正方体，如图所示；
当正视图为正方形时，其面积最小${（\sqrt{2}）}^{2}$=2；
当正视图为对角面时，其面积最大为$\sqrt{2}$×$\sqrt{{（\sqrt{2}）}^{2}{+（\sqrt{2}）}^{2}}$=2$\sqrt{2}$．
∴满足棱长为$\sqrt{2}$的正方体的正视图面积的范围为[2，2$\sqrt{2}$]．
∴B、C、D都有可能，
A中$\sqrt{2}$-1＜2，∴A不可能．
故选：A．

点评 本题考查了空间几何体的三视图的应用问题，也考查了空间想象能力的应用问题，是基础题目．