
 设数列{xn}的各项都为正数且x1=1.如图,△ABC所在平面上的点Pn (n∈N*)均满足△PnAB与△PnAC的面积比为3:1,若$\overrightarrow{{P_n}A}=\frac{1}{3}{x_{n+1}}\overrightarrow{{P_n}B}-(2{x_n}+1)\overrightarrow{{P_n}C}$,则x5的值为( )
设数列{xn}的各项都为正数且x1=1.如图,△ABC所在平面上的点Pn (n∈N*)均满足△PnAB与△PnAC的面积比为3:1,若$\overrightarrow{{P_n}A}=\frac{1}{3}{x_{n+1}}\overrightarrow{{P_n}B}-(2{x_n}+1)\overrightarrow{{P_n}C}$,则x5的值为( )| A. | 31 | B. | 33 | C. | 61 | D. | 63 |
分析 先得到$\overrightarrow{{P}_{n}A}+(2{x}_{n}+1)\overrightarrow{{P}_{n}C}$=$\frac{1}{3}{x}_{n+1}\overrightarrow{{P}_{n}B}$,作出平行四边形PnAED,其中$\overrightarrow{{P}_{n}D}=(2{x}_{n}+1)\overrightarrow{{P}_{n}C}$,$\overrightarrow{{P}_{n}E}=\frac{1}{3}{x}_{n+1}\overrightarrow{{P}_{n}B}$,能够得到$\frac{{S}_{△{P}_{n}AC}}{{S}_{△{P}_{n}AE}}=\frac{1}{2{x}_{n}+1}$,$\frac{{S}_{△{P}_{n}AE}}{{S}_{△{P}_{n}AB}}=\frac{1}{3}{x}_{n+1}$,从而便得到$\frac{{S}_{△{P}_{n}AC}}{{S}_{△{P}_{n}AB}}=\frac{{x}_{n+1}}{3(2{x}_{n}+1)}=\frac{1}{3}$.这样即可得到xn+1+1=2(xn+1),从而数列{an+1}是以2为首项,2为公比的等比数列,从而可求出x5.
解答 解:由$\overrightarrow{{P}_{n}A}=\frac{1}{3}{x}_{n+1}\overrightarrow{{P}_{n}B}$$-(2{x}_{n}+1)\overrightarrow{{P}_{n}C}$得,$\overrightarrow{{P}_{n}A}+(2{x}_{n}+1)\overrightarrow{{P}_{n}C}$=$\frac{1}{3}{x}_{n+1}\overrightarrow{{P}_{n}B}$;
用图形表示上面等式如下: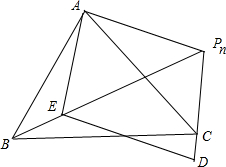 其中$\overrightarrow{{P}_{n}D}=(2{x}_{n}+1)\overrightarrow{{P}_{n}C}$,$\overrightarrow{{P}_{n}E}=\frac{1}{3}{x}_{n+1}\overrightarrow{{P}_{n}B}$;
其中$\overrightarrow{{P}_{n}D}=(2{x}_{n}+1)\overrightarrow{{P}_{n}C}$,$\overrightarrow{{P}_{n}E}=\frac{1}{3}{x}_{n+1}\overrightarrow{{P}_{n}B}$;
∴$\frac{|\overrightarrow{{P}_{n}E}|}{|\overrightarrow{{P}_{n}B}|}=\frac{1}{3}{x}_{n+1}$,∴$\frac{{S}_{△{P}_{n}AE}}{{S}_{△{P}_{n}AB}}=\frac{1}{3}{x}_{n+1}$;
∵$\frac{|\overrightarrow{{P}_{n}C}|}{|\overrightarrow{{P}_{n}D}|}=\frac{|{P}_{n}C|}{|AE|}=\frac{1}{2{x}_{n}+1}$;
∴$\frac{{S}_{△{P}_{n}AC}}{{S}_{△{P}_{n}AE}}=\frac{1}{2{x}_{n}+1}$;
∴$\frac{{S}_{△{P}_{n}AC}}{{S}_{△{P}_{n}AB}}=\frac{{x}_{n+1}}{3(2{x}_{n}+1)}=\frac{1}{3}$;
∴xn+1=2xn+1;
∴xn+1+1=2(xn+1);
∴{xn+1}构成以2为首项,2为公比的等比数列;
∴${x}_{5}+1=2•{2}^{4}$;
∴x5=31.
故选A.
点评 考查向量加法的平行四边形法则,数乘的几何意义,两个三角形面积的比和底边的比,或高的比的关系,以及等比数列的定义,等比数列的通项公式.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:选择题
| A. | 81 | B. | 99 | C. | 108 | D. | 117 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 良好 | 合格 | |
| 男 | 180 | 70 | 20 |
| 女 | 120 | a | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,圆O的直径为AB,半径OC垂直于AB,M为AO上一点,CM的延长线交圆O于N,过N点的切线交BA的延长线于P.
如图,圆O的直径为AB,半径OC垂直于AB,M为AO上一点,CM的延长线交圆O于N,过N点的切线交BA的延长线于P.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}-1$ | B. | 2 | C. | $\sqrt{2}+1$ | D. | $2\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com