考点:指、对数不等式的解法
专题:导数的综合应用,不等式的解法及应用
分析:由不等式中的对数式的真数大于0求得x的初步范围,把不等式转化为(x+1)ln2(x+1)-x2-1),然后换元令x+1=t(t>0),通过两次求导后构造函数g(t)=lnt-t+1(t>0),再由导数研究其最值,得到y在(0,1)上为增函数,在(1,+∞)上为减函数,进一步把原不等式等价于y<0?t≠1?x+1≠1?x≠0.结合x>-1求得原不等式的解集.
解答:
解:由已知得x>-1,
∴原不等式化为(x+1)ln
2(x+1)-x
2<0,
令f(x)=(x+1)ln
2(x+1)-x
2(x>-1),
再令x+1=t(t>0),
y=f(t)=tln
2t-(t-1)
2(t>0),
y′=ln2t+2t•lnt-2(t-1)=ln
2t+2lnt-2t+2(t>0),
y′′=lnt+-2=
(lnt+1-t)(t>0),
令g(t)=lnt-t+1(t>0),
g′(t)=-1=(t>0),
由g′(t)>0⇒0<t<1,g′(t)<0⇒t>1.
∴g(t)在(0,1)上为增函数,在(1,+∞)上为减函数,
∴g(t)
max=g(1)=ln1+1-1=0.
∴g(t)≤0,
∴
y′′=g(t)≤0.
则y′在(0,+∞)上单调递减,
又
y′|t=1=(ln1+1-1)=0,
∴0<t<1时,y′>0,t>1时y′<0.
∴y在(0,1)上为增函数,在(1,+∞)上为减函数,
∴
ymax=1•ln21-(1-1)2=0.
∴原不等式等价于y<0?t≠1?x+1≠1?x≠0.
由x>-1,
∴原不等式的解集为(-1,0)∪(0,+∞).
故答案为:(-1,0)∪(0,+∞).
点评:本题考查了含有对数式的不等式的解法,考查了数学转化思想方法,训练了利用导数判断函数的单调性和求函数的最值,属难度较大的题目.



 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案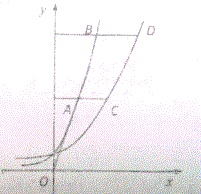 如图,A,B是函数y=e2x的图象上两点,分别过A B作x轴的平行线与函数y=ex的图象交于C,D两点.
如图,A,B是函数y=e2x的图象上两点,分别过A B作x轴的平行线与函数y=ex的图象交于C,D两点.