
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
分析 根据向量的模和向量的夹角公式,分类讨论求出△ABC是钝角三角形的k的范围,再根据概率公式计算即可.
解答 解:∵|${\overrightarrow{AB}}$|=$\sqrt{1+{k}^{2}}$<$\sqrt{10}$,
∴-3<k<3,
∵$\overrightarrow{BC}$=$\overrightarrow{AC}$-$\overrightarrow{AB}$=(2-k,3),
若$\overrightarrow{AB}•\overrightarrow{AC}$<0,即2k+4<0,解得-3<k<-2,
若$\overrightarrow{AB}$•$\overrightarrow{CB}$<0,即k(k-2)-1×3<0,解得-1<k<3,
若$\overrightarrow{AC}$•$\overrightarrow{BC}$<0,即2(2-k)+3×4<0,解得k>8舍去,
∴△ABC是钝角三角形的概率P=$\frac{-2+3+3+1}{3-(-3)}$=$\frac{5}{6}$,
故选:D
点评 本题考查了几何概型概率问题,关键求出满足条件的长度,属于中档题.


科目:高中数学 来源: 题型:解答题
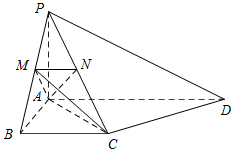 如图,PA⊥平面ABCD,AB⊥AD,AD∥BC,PA=AB=BC,AD=2AB,点M,N分别在PB,PC上,且MN∥BC.
如图,PA⊥平面ABCD,AB⊥AD,AD∥BC,PA=AB=BC,AD=2AB,点M,N分别在PB,PC上,且MN∥BC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
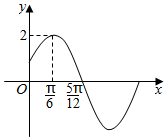 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示查看答案和解析>>
科目:高中数学 来源: 题型:填空题
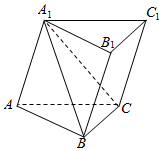 如图,三棱柱ABC-A1B1C1的体积为V1,四棱锥A1-BCC1B1的体积为V2,则$\frac{V_1}{V_2}$=$\frac{3}{2}$.
如图,三棱柱ABC-A1B1C1的体积为V1,四棱锥A1-BCC1B1的体积为V2,则$\frac{V_1}{V_2}$=$\frac{3}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,平面ABCD⊥平BCEF,且四边形ABC为矩形,四边形BCEF为直角梯形,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2.
如图所示,平面ABCD⊥平BCEF,且四边形ABC为矩形,四边形BCEF为直角梯形,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com