
| A. | 若α∥β,l?α,n?β,则l∥n | B. | 若α⊥β,l?α,则l⊥β | ||
| C. | 若l⊥α,l∥β,则α⊥β | D. | 若l⊥n,m⊥n,则l∥m |
分析 对于A,根据面面平行的性质定理判断命题错误;
对于B,根据面面垂直的性质定理判断命题错误;
对于C,根据线面垂直的性质定理与面面垂直的判定定理,证明命题正确;
对于D,根据两条直线的位置关系与线线垂直的判定问题,得出命题错误.
解答 解:对于A,α∥β与直线l、n的位置关系无关,所以直线l、n的位置关系不确定,A错误;
对于B,由α⊥β,l?α,得出l⊥β或l∥β或l?β,所以B错误;
对于C,由l⊥α,l∥β,过l作平面γ∩β=a,
所以l∥a,所以a⊥α,从而β⊥α,C正确;
对于D,m⊥n,l⊥n,直线m、l的位置关系是平行或相交或异面,所以D错误.
故选:C.
点评 本题考查了空间直线位置关系问题,考查了面面平行的判定,线面垂直的判定以及空间想象能力与逻辑思维能力,是基础题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2sin(3x-$\frac{π}{6}$) | B. | y=2sin(3x+$\frac{π}{6}$) | C. | y=2sin($\frac{x}{3}$+$\frac{π}{6}$) | D. | y=2sin($\frac{x}{3}$-$\frac{π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x4 | B. | f(x)=x+$\frac{1}{x}$ | C. | f(x)=x3-1 | D. | f(x)=$\frac{1}{{x}^{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3) | B. | (-∞,-1) | C. | (-1,1) | D. | (-3,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
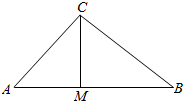 设a,b,c分别是△ABC中角A,B,C的对边
设a,b,c分别是△ABC中角A,B,C的对边查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com