已知x=3是函数f(x)=(x2+ax-2a-3)e3-x的极值点.
(1)求f(x)的单调区间(用a表示);
(2)设a>0,g(x)=(a2+8)ex,若存在ξ1,ξ2∈[0,4]使得|f(ξ1)-g(ξ2)|<3成立,求a的取值范围.
解:(1)f′(x)=(2x+a)e
3-x+(x
2+ax-2a-3)(-1)e
3-x
=[-x
2+(2-a)x+3a+3]e
3-x=-[x
2+(a-2)x-3(a+1)]e
3-x
=-(x-3)[x+(a+1)]e
3-x…(3分)
∵x=3是函数f(x)的极值点
∴-(a+1)≠3即a≠-4
(i)当-(a+1)<3即a>-4时
当x∈(-∞,-a-1]和[3,+∞)时,f′(x)≤0,f(x)单调递减
当x∈(-a-1,3)时,f′(x)>0,f(x)单调递增.…(5分)
(ii)当-(a+1)>3即a<-4时
当x∈(-∞,3]和[-a-1,+∞)时,f′(x)≤0,f(x)单调递减
当x∈(3,-a-1)时,f′(x)>0,f(x)单调递增.…(7分)
(2)∵a>0,∴-(a+1)<0
∴当x∈[0,3]时f(x)单调递增,当x∈[3,4]时f(x)单调递减
∴当x∈[0,4]时,f
max(x)=f(3)=a+6…(9分)
∵g(x)=(a
2+8)e
x在x∈[0,4]时是增函数,g
min(x)=g(0)=a
2+8…(11分)
又∵
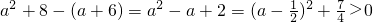
∴g
min(x)>f
max(x),∴当x∈[0,4]时,g(x)>f(x)恒成立.
∴若存在ξ
1,ξ
2∈[0,4]使得|f(ξ
1)-g(ξ
2)|<3
只要g
min(x)-f
max(x)<3即可…(14分)
即

所以a的取值范围为
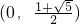
.…(15分)
分析:(1)先求导函数,利用x=3是函数f(x)的极值点,可得-(a+1)≠3即a≠-4,进而分a>-4与a<-4,分类讨论,研究函数的单调性;
(2)分别求出g
min(x)与f
max(x),再将问题等价转化为:若存在ξ
1,ξ
2∈[0,4]使得|f(ξ
1)-g(ξ
2)|<3,只要g
min(x)-f
max(x)<3即可,从而解不等式,即可求出a的取值范围.
点评:本题以函数的极值为载体,考查导数的运用,考查利用导数求函数的单调区间,同时考查学生分析解决问题的能力.

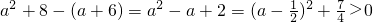

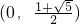 .…(15分)
.…(15分)
