
【题目】已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,且曲线
轴的正半轴为极轴建立极坐标系,且曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若直线![]() 的斜率为
的斜率为![]() ,判断直线
,判断直线![]() 与曲线
与曲线![]() 的位置关系;
的位置关系;
(2)求![]() 与
与![]() 交点的极坐标(
交点的极坐标(![]() ,
,![]() ).
).
科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.

(1)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取
的芒果中随机抽取![]() 个,再从这
个,再从这![]() 个中随机抽取
个中随机抽取![]() 个,记随机变量
个,记随机变量![]() 表示质量在
表示质量在![]() 内的芒果个数,求
内的芒果个数,求![]() 的分布列及数学期望.
的分布列及数学期望.
(2)以各组数据的中间数代表这组数据的平均值,将频率视为概率,某经销商来收购芒果,该种植园中还未摘下的芒果大约还有![]() 个,经销商提出如下两种收购方案:
个,经销商提出如下两种收购方案:
A:所以芒果以![]() 元/千克收购;
元/千克收购;
B:对质量低于![]() 克的芒果以
克的芒果以![]() 元/个收购,高于或等于
元/个收购,高于或等于![]() 克的以
克的以![]() 元/个收购.
元/个收购.
通过计算确定种植园选择哪种方案获利更多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,以短轴端点和焦点为顶点的四边形的周长为
,以短轴端点和焦点为顶点的四边形的周长为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程及焦点坐标.
的标准方程及焦点坐标.
(Ⅱ)过椭圆![]() 的右焦点作
的右焦点作![]() 轴的垂线,交椭圆于
轴的垂线,交椭圆于![]() 、
、![]() 两点,过椭圆上不同于点
两点,过椭圆上不同于点![]() 、
、![]() 的任意一点
的任意一点![]() ,作直线
,作直线![]() 、
、![]() 分别交
分别交![]() 轴于
轴于![]() 、
、![]() 两点.证明:点
两点.证明:点![]() 、
、![]() 的横坐标之积为定值.
的横坐标之积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为正方形,侧面PAD是正三角形,侧面![]() 底面ABCD,M是PD的中点.
底面ABCD,M是PD的中点.

(1)求证:![]() 平面PCD;
平面PCD;
(2)求侧面PBC与底面ABCD所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分
布直方图:

(1)依据频率分布直方图估算该运动员投篮命中时,他到篮筐中心的水平距离的中位数;
(2)若从该运动员投篮命中时,他到篮筐中心的水平距离为2到5米的这三组中,用分层抽样的方法抽取7次成绩(单位:米,运动员投篮命中时,他到篮筐中心的水平距离越远越好),并从抽到的这7次成绩中随机抽取2次.规定:这2次成绩均来自到篮筐中心的水平距离为4到5米的这一组,记 1分,否则记0分.求该运动员得1分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:![]() =2px(p>0)的准线方程为x=-
=2px(p>0)的准线方程为x=-![]() ,F为抛物线的焦点
,F为抛物线的焦点
(I)求抛物线C的方程;
(II)若P是抛物线C上一点,点A的坐标为(![]() ,2),求
,2),求![]() 的最小值;
的最小值;
(III)若过点F且斜率为1的直线与抛物线C交于M,N两点,求线段MN的中点坐标。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为抛物线
为抛物线![]() 的焦点,
的焦点,![]() 为抛物线
为抛物线![]() 上三点,且点
上三点,且点![]() 在第一象限,直线
在第一象限,直线![]() 经过点
经过点![]() 与抛物线
与抛物线![]() 在点
在点![]() 处的切线平行,点
处的切线平行,点![]() 为
为![]() 的中点.
的中点.
(1)证明:![]() 与
与![]() 轴平行;
轴平行;
(2)求![]() 面积
面积![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市规定,高中学生在校期间须参加不少于80小时的社区服务才合格.某校随机抽取20位学生参加社区服务的数据,按时间段![]() (单位:小时)进行统计,其频率分布直方图如图所示.
(单位:小时)进行统计,其频率分布直方图如图所示.
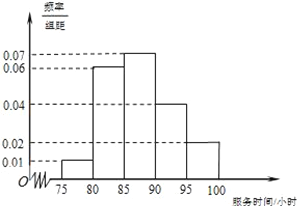
(1)求抽取的20人中,参加社区服务时间不少于90小时的学生人数;
(2)从参加社区服务时间不少于90小时的学生中任意选取2人,求所选学生的参加社区服务时间在同一时间段内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com