
分析 (1)求出函数的对数,得到关于x0的方程,解出即可;
(2)令g(x)=$\frac{f(x)}{x}$,只需证明g(x)>0即可,根据函数的单调性证出结论;
(3)问题等价于$\frac{e^x}{x^2}-b=0$.注意x≠0.令$H(x)=\frac{e^x}{x^2}-b$,通过讨论b的范围,根据函数的单调性判断即可.
解答 (1)解:$f'(x)=\frac{{{e^x}x-{e^x}}}{x^2}$. 因为切线ax-y=0过原点(0,0),
所以 $\frac{{{e^{x_0}}{x_0}-{e^{x_0}}}}{x_0^2}=\frac{{\frac{{{e^{x_0}}}}{x_0}}}{x_0}$,解得:x0=2.
(2)证明:设$g(x)=\frac{f(x)}{x}=\frac{e^x}{x^2}(x>0)$,则$g'(x)=\frac{{{e^x}({x^2}-2x)}}{x^4}$.
令$g'(x)=\frac{{{e^x}({x^2}-2x)}}{x^4}=0$,解得x=2,
令g′(x)>0,解得:x>2,令g′(x)<0,解得:0<x<2,
∴g(x)的最小值是g(2)=$\frac{{e}^{2}}{4}$>1,
故x>0时,f(x)>x;
(3)解:F(x)=0等价于f(x)-bx=0,等价于$\frac{e^x}{x^2}-b=0$.注意x≠0.
令$H(x)=\frac{e^x}{x^2}-b$,所以$H'(x)=\frac{{{e^x}(x-2)}}{x^3}(x≠0)$.
( I)当b≤0时,H(x)>0,所以H(x)无零点,即F(x)定义域内无零点.
( II)当b>0时,( i)当x<0时,H'(x)>0,H(x)单调递增;
因为H(x)在(-∞,0)上单调递增,而$H(-\frac{1}{{\sqrt{b}}})=b{e^{-\frac{1}{{\sqrt{b}}}}}-b=b•\frac{{1-{e^{\frac{1}{{\sqrt{b}}}}}}}{{{e^{\frac{1}{{\sqrt{b}}}}}}}$,
又${e^{\frac{1}{{\sqrt{b}}}}}>1$,所以$H(-\frac{1}{{\sqrt{b}}})<0$.
又因为$H(-\frac{1}{{\sqrt{nb}}})=nb{e^{-\frac{1}{{\sqrt{nb}}}}}-b=b•\frac{{n-{e^{\frac{1}{{\sqrt{nb}}}}}}}{{{e^{\frac{1}{{\sqrt{nb}}}}}}}$,其中n∈N*,
取$n=[{\frac{1}{b}}]+3$,$[{\frac{1}{b}}]$表示$\frac{1}{b}$的整数部分,
所以$1<{e^{\frac{1}{{\sqrt{nb}}}}}<e$,n>3,由此$H(-\frac{1}{{\sqrt{nb}}})>0$.
由零点存在定理知,H(x)在(-∞,0)上存在唯一零点.
( ii)当0<x<2时,H'(x)<0,H(x)单调递减;
当x>2时,H'(x)>0,H(x)单调递增.
所以当x=2时,H(x)有极小值也是最小值,$H(2)=\frac{e^2}{4}-b$.
①当$H(2)=\frac{e^2}{4}-b>0$,即$0<b<\frac{e^2}{4}$时,H(x)在(0,+∞)上不存在零点;
②当$H(2)=\frac{e^2}{4}-b=0$,即$b=\frac{e^2}{4}$时,H(x)在(0,+∞)上存在惟一零点2;…(12分)
③当$H(2)=\frac{e^2}{4}-b<0$,即$b>\frac{e^2}{4}$时,由${e^{\frac{1}{{\sqrt{b}}}}}>1$有$H(\frac{1}{{\sqrt{b}}})=b{e^{\frac{1}{{\sqrt{b}}}}}-b=b({e^{\frac{1}{{\sqrt{b}}}}}-1)>0$,
而H(2)<0,所以H(x)在(0,2)上存在惟一零点;
又因为2b>3,$H(2b)=\frac{{{e^{2b}}}}{{4{b^2}}}-b=\frac{{{e^{2b}}-4{b^3}}}{{4{b^2}}}$.
令$h(t)={e^t}-\frac{1}{2}{t^3}$,其中t=2b>2,$h'(t)={e^t}-\frac{3}{2}{t^2}$,h''(t)=et-3t,h'''(t)=et-3,
所以h'''(t)>e2-3>0,因此h''(t)在(2,+∞)上单调递增,从而h''(t)>h(2)=e2-6>0,
所以h'(t)在(2,+∞)上单调递增,因此h'(t)>h'(2)=e2-6>0,
故h(t)在(2,+∞)上单调递增,所以h(t)>h(2)=e2-4>0.
由上得H(2b)>0,由零点存在定理知,H(x)在(2,2b)上存在惟一零点,
即在(2,+∞)上存在唯一零点.
综上所述:当$a_n^2={S_{2n-1}}$时,函数F(x)的零点个数为0;
当∵${b_n}=\frac{1}{{{a_n}{a_{n+1}}}}=\frac{1}{(2n-1)(2n+1)}=\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$时,函数F(x)的零点个数为1;
当∵时,函数F(x)的零点个数为2;
当∴$\frac{{{a_1}+{a_{2n-1}}}}{2}={a_n}$时,函数F(x)的零点个数为3.
点评 本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用、不等式的证明以及函数零点问题,是一道综合题.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
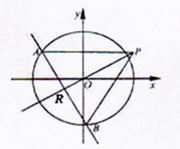 如图,椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{1}{2}$,其左焦点到椭圆上点的最远距离为3,点P(2,1)为椭圆外一点,不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分
如图,椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{1}{2}$,其左焦点到椭圆上点的最远距离为3,点P(2,1)为椭圆外一点,不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com