
分析 (1)用比较法证明不等式,(x3+y3 )-(x2y+xy2)=(x+y)(x-y)2,分析符号可得结论.
(2)利用作差法,易证3(a3+b3+c3)-(a2+b2+c2)(a+b+c)=(a+b)(a-b)2+(b+c)(b-c)2+(a+c)(a-c)2,又a,b,c>0,从而可得a3+b3+c3≥$\frac{1}{3}$(a2+b2+c2)(a+b+c).
解答 证明:(1)∵(x3+y3 )-(x2y+xy2)=x2 (x-y)+y2(y-x)=(x-y)(x2-y2 )
=(x+y)(x-y)2.
∵x,y都是正实数,∴(x-y)2≥0,(x+y)>0,∴(x+y)(x-y)2≥0,
∴x3+y3≥x2y+xy2.
(2)3(a3+b3+c3)-(a2+b2+c2)(a+b+c)
=3(a3+b3+c3)-(a3+b3+c3+a2b+b2a+a2c+c2a+b2c+c2b)
=[(a3+b3)-(a2b+b2a)]+[(b3+c3)-(b2c+c2b)]+[(a3+c3)-(a2c+c2a)],
=[(a+b)(a2-ab+b2)-ab(a+b)]+[(b+c)(b2-bc+c2)-bc(b+c)]+[(a+c)(a2-ac+c2)-ac(a+c)]
=(a+b)(a-b)2+(b+c)(b-c)2+(a+c)(a-c)2,
∵a,b,c>0,
∴a+b>0,(a-b)2≥0,
∴(a+b)(a-b)2≥0,同理可得(b+c)(b-c)2≥0,(a+c)(a-c)2≥0,
∴(a+b)(a-b)2+(b+c)(b-c)2+(a+c)(a-c)2≥0,
∴a3+b3+c3≥$\frac{1}{3}$(a2+b2+c2)(a+b+c).
点评 本题考查用比较法、作差法证明不等式,基本不等式的应用,将式子变形是证明的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
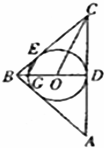 已知圆O是△ABC的内切圆,与AC,BC分别切于D,E两点,如图所示,连接BD交圆O于点G,BC=BA=2$\sqrt{2}$,AC=4
已知圆O是△ABC的内切圆,与AC,BC分别切于D,E两点,如图所示,连接BD交圆O于点G,BC=BA=2$\sqrt{2}$,AC=4 查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com