
【题目】已知O为原点,抛物线![]() 的准线与y轴的交点为H,P为抛物线C上横坐标为4的点,已知点P到准线的距离为5.
的准线与y轴的交点为H,P为抛物线C上横坐标为4的点,已知点P到准线的距离为5.
(1)求C的方程;
(2)过C的焦点F作直线l与抛物线C交于A,B两点,若以AH为直径的圆过B,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】新冠疫情发生后,酒精使用量大增,某生产企业调整设备,全力生产![]() 与
与![]() 两种不同浓度的酒精,按照计划可知在一个月内,酒精日产量
两种不同浓度的酒精,按照计划可知在一个月内,酒精日产量![]() (单位:吨)与时间n(
(单位:吨)与时间n(![]() 且
且![]() )成等差数列,且
)成等差数列,且![]() ,
,![]() .又知
.又知![]() 酒精日产量所占比重
酒精日产量所占比重![]() 与时间n成等比数列,
与时间n成等比数列,![]() 酒精日产量所占比重与时间n的关系如下表(
酒精日产量所占比重与时间n的关系如下表(![]() ):
):
|
|
|
| …… |
时间n | 1 | 2 | 3 | …… |
(1)求![]() ,
,![]() 的通项公式;
的通项公式;
(2)若![]() ,求前n天
,求前n天![]() (单位:吨,
(单位:吨,![]() 且
且![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学的学生积极参加体育锻炼,其中有96%的学生喜欢足球或游泳,60%的学生喜欢足球,82%的学生喜欢游泳,则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是( )
A.62%B.56%
C.46%D.42%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,且过点A(2,1).
,且过点A(2,1).
(1)求C的方程:
(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足.证明:存在定点Q,使得|DQ|为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司采购了一批零件,为了检测这批零件是否合格,从中随机抽测120个零件的长度(单位:分米),按数据分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 这6组,得到如图所示的频率分布直方图,其中长度大于或等于1.59分米的零件有20个,其长度分别为1.59,1.59,1.61,1.61,1.62,1.63,1.63,1.64,1.65,1.65,1.65,1.65,1.66,1.67,1.68,1.69,1.69,1.71,1.72,1.74,以这120个零件在各组的长度的频率估计整批零件在各组长度的概率.
这6组,得到如图所示的频率分布直方图,其中长度大于或等于1.59分米的零件有20个,其长度分别为1.59,1.59,1.61,1.61,1.62,1.63,1.63,1.64,1.65,1.65,1.65,1.65,1.66,1.67,1.68,1.69,1.69,1.71,1.72,1.74,以这120个零件在各组的长度的频率估计整批零件在各组长度的概率.
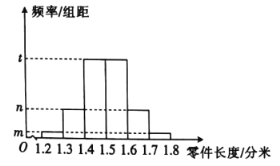
(1)求这批零件的长度大于1.60分米的频率,并求频率分布直方图中![]() ,
,![]() ,
,![]() 的值;
的值;
(2)若从这批零件中随机选取3个,记![]() 为抽取的零件长度在
为抽取的零件长度在![]() 的个数,求
的个数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)若变量![]() 满足
满足![]() 且
且![]() ,则称变量
,则称变量![]() 满足近似于正态分布
满足近似于正态分布![]() 的概率分布.如果这批零件的长度
的概率分布.如果这批零件的长度![]() (单位:分米)满足近似于正态分布
(单位:分米)满足近似于正态分布![]() 的概率分布,则认为这批零件是合格的将顺利被签收;否则,公司将拒绝签收.试问,该批零件能否被签收?
的概率分布,则认为这批零件是合格的将顺利被签收;否则,公司将拒绝签收.试问,该批零件能否被签收?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以直角坐标系的原点
为参数).以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立坐标系,曲线
轴的正半轴为极轴建立坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com