
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)试判断函数![]() 的单调性;
的单调性;
(Ⅱ)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析; (Ⅱ) ![]()
【解析】
(Ⅰ)求出原函数的导函数,然后对a分类,当a≤0时,![]() <0,f(x)为R上的减函数;当a>0时,由导函数为0求得导函数的零点,再由导函数的零点对定义域分段,根据导函数在各段内的符号得到原函数的单调性;
<0,f(x)为R上的减函数;当a>0时,由导函数为0求得导函数的零点,再由导函数的零点对定义域分段,根据导函数在各段内的符号得到原函数的单调性;
(Ⅱ)分离参数t,可得![]() 恒成立.令
恒成立.令![]() ,则问题等价于求解函数g(x)的最小值,然后利用导数分析求解函数g(x)的最小值得答案.
,则问题等价于求解函数g(x)的最小值,然后利用导数分析求解函数g(x)的最小值得答案.
(Ⅰ)由题可得函数![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
当![]() 时,因为
时,因为![]() ,所以
,所以![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,令
时,令![]() ,解得
,解得![]() ;令
;令![]() ,解得
,解得![]() ,
,
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
综上,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减;当
上单调递减;当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(Ⅱ)当![]() 时,
时,![]() ,
,
则不等式![]() 可化为
可化为![]() ,
,
因为不等式![]() 恒成立,所以原问题可转化为
恒成立,所以原问题可转化为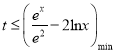 .
.
设![]() ,显然函数
,显然函数![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
令![]() ,则
,则![]() 恒成立,
恒成立,
所以函数![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,所以当
,所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() ,所以
,所以![]() ,
,
故实数![]() 的取值范围为
的取值范围为![]() .
.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】某公司的甲、乙两名工程师因为工作需要,各自选购一台笔记本电脑.该公司提供了![]() 三款笔记本电脑作为备选,这三款笔记本电脑在某电商平台的销量和用户评分如下表所示:
三款笔记本电脑作为备选,这三款笔记本电脑在某电商平台的销量和用户评分如下表所示:
型号 |
|
|
|
销量(台) | 2000 | 2000 | 4000 |
用户评分 | 8 | 6.5 | 9.5 |
若甲选购某款笔记本电脑的概率与对应的销量成正比,乙选购某款笔记本电脑的概率与对应的用户评分减去5的值成正比,且他们两人选购笔记本电脑互不影响.
(1)求甲、乙两人选购不同款笔记本电脑的概率;
(2)若公司给购买这三款笔记本电脑的员工一定的补贴,补贴标准如下表:
型号 |
|
|
|
补贴(千元) | 3 | 4 | 5 |
记甲、乙两人获得的公司补贴之和为![]() 千元,求
千元,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年世界海洋日暨全国海洋宣传日主场活动在海南三亚举行,此次活动主题为“珍惜海洋资源保护海洋生物多样性”,旨在进一步提高公众对节约利用海洋资源、保护海洋生物多样性的认识,为保护蓝色家园做出贡献.联合国于第63届联合国大会上将每年的6月8日确定为“世界海洋日”,为了响应世界海洋日的活动,2019年12月北京某高校行政主管部门从该大学随机抽取部分大学生进行一次海洋知识测试,并根据被测验学生的成绩(得分都在区间![]() 内)绘制成如图所示的频率分布直方图.
内)绘制成如图所示的频率分布直方图.

(1)试求被测验大学生得分的中位数(保留到整数);
(2)若学生的得分成绩不低于80分的认为是“成绩优秀”,现在从认为“成绩优秀”的学生中根据原有分组按照分层抽样的方法抽取10人进行奖励,最后再从这10人中随机选取3人作为优秀代表发言.
①求所抽取的3人不属于同一组的概率;
②记这3人中,![]() 为测试成绩在
为测试成绩在![]() 内的人数,求
内的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对n个互不相等的正整数,其中任意六个数中都至少存在两个数,使得其中一个能整除另一个.求n的最小值,使得在这n个数中一定存在六个数,其中一个能被另外五个整除.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】离心率![]() 的椭圆
的椭圆![]() 的中心在坐标原点
的中心在坐标原点![]() ,焦点在
,焦点在![]() 轴上.过点
轴上.过点![]() 的斜率为
的斜率为![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() 、
、![]() ,且满足
,且满足![]() .
.
(1)固定![]() ,当
,当![]() 的面积取得最大值时,求椭圆
的面积取得最大值时,求椭圆![]() 的方程;
的方程;
(2)若![]() 变化,且
变化,且![]() ,试问:实数
,试问:实数![]() 和
和![]() 分别为何值时,椭圆
分别为何值时,椭圆![]() 的长轴长取得最大值?并求出此时椭圆的方程.
的长轴长取得最大值?并求出此时椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全体非负整数0,1,2,…,按其自然顺序组成一个小数![]() 456 789 101 112 131 415 161 718 19 ….问:
456 789 101 112 131 415 161 718 19 ….问:![]() 是否为无理数?证明你的结论.
是否为无理数?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆的方程![]() ,从0,3,4,5,6,7,8,9,10这九个数中选出3个不同的数,分别作圆心的横坐标、纵坐标和圆的半径.问:
,从0,3,4,5,6,7,8,9,10这九个数中选出3个不同的数,分别作圆心的横坐标、纵坐标和圆的半径.问:
(1)可以作多少个不同的圆?
(2)经过原点的圆有多少个?
(3)圆心在直线上![]() 的圆有多少个?
的圆有多少个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四个小球,分别写有“海”“中”“加”“油”四个字,有放回地从中任取一个小球,取到“加”就停止,用随机模拟的方法估计直到第二次停止的概率:先由计算器产生1到4之间取整数值的随机数,且用1、2、3、4表示取出小球上分别写有“海”“中”“加”“油”四个字,以每两个随机数为一组,代表两次的结果.经随机模拟产生了20组随机数:
13 24 12 32 43 14 24 32 31 21
23 13 32 21 24 42 13 32 21 34
据此估计,直到第二次就停止概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com