（本题满分16分）
已知椭圆
的左焦点为
,离心率为
，点M在椭圆上且位于第一象限，直线FM被圆
截得的线段的长为c，
.
（Ⅰ）求直线FM的斜率；
（Ⅱ）求椭圆的方程；
（Ⅲ）设椭圆上动点P在x轴上方，若直线FP的斜率大于
，求直线OP（O为原点）的斜率的取值范围.
活力试卷系列答案
课课优能力培优100分系列答案科目：高中数学 来源：2016届甘肃省高三上学期期中理科数学试卷（解析版） 题型：解答题
（本小题满分10分）选修4～1:几何证明选讲
如图，AB是⊙O的一条切线，切点为B，直线ADE，CFD，CGE都是⊙O的割线，已知AC=AB．
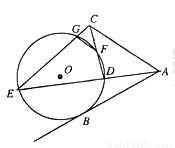
（1）若CG=1，CD=4，求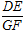
的值；
（2）求证：FG//AC．
查看答案和解析>>
科目：高中数学 来源：2015-2016学年江苏省泰州市姜堰区高二上学期期中考试理科数学试卷（解析版） 题型：解答题
（本题满分14分）
在平面直角坐标系xOy中，椭圆C的参数方程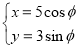
(φ为参数)，直线
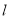的参数方程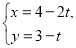
(t为参数) ．
（I）求C与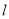
的普通方程；
（II）求过C的右焦点，且平行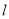的直线方程．
查看答案和解析>>
科目：高中数学 来源：2015-2016学年湖北省黄石市高一10月月考数学试卷（解析版） 题型：填空题
已知定义在R上的偶函数f（x），当x＞0时，f（x）＝－x3＋1，则f（－2）与f（3）的乘积为________
查看答案和解析>>
科目：高中数学 来源：2015-2016学年安徽省阜阳市高二上第一次调研考文科数学试卷（解析版） 题型：解答题
某渔业公司今年初用98万元购进一艘渔船用于捕捞，第一年需各种费用12万元，从第二年开始包括维修费在内，每年所需费用均比上一年增加4万元，该船每年捕捞的总收入为50万元．
（1）该船捕捞几年开始盈利？（即总收入减去成本及所有费用之差为正值）
（2）该船捕捞若干年后，处理方案有两种：
①当年平均盈利达到最大值时，以26万元的价格卖出；
②当盈利总额达到最大值时，以8万元的价格卖出．问哪一种方案较为合算，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的值域是
，则函数
的值域为（ ）
（B）
（C）
（D）
的定义域为
，函数
的值域为
.
,
； 
,
是偶函数，则
的递减区间是________
，则
的值是（ ）
B、
C、
D、不确定