
设定点M(3, )与抛物线
)与抛物线 =2x上的点P的距离为
=2x上的点P的距离为 ,P到抛物线准线l的距为
,P到抛物线准线l的距为 ,则
,则 +
+ 取最小值时,P点的坐标为
取最小值时,P点的坐标为
| A.(0,0) | B.(1, ) ) | C.(2,2) | D.( ,- ,- ) ) |
C
解析试题分析:先判断出M(3, )在抛物线
)在抛物线 =2x的外部然后做出图形(如下图)则PM=d1过p作PN⊥直线x=
=2x的外部然后做出图形(如下图)则PM=d1过p作PN⊥直线x= 则PN=d2,根据抛物线的定义可得d1+d2=PM+PF故要使
则PN=d2,根据抛物线的定义可得d1+d2=PM+PF故要使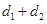 取最小值则只有当P,M,F三点共线时成立因此可求出MF所在的直线方程然后与抛物线的方程联立即可求出P点的坐标.
取最小值则只有当P,M,F三点共线时成立因此可求出MF所在的直线方程然后与抛物线的方程联立即可求出P点的坐标.
∵(3,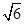 )在抛物线
)在抛物线 =2x上且
=2x上且 >
>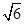 ∴M(3,
∴M(3, )在抛物线
)在抛物线 =2x的外部,∵抛物线y2=2x的焦点F(
=2x的外部,∵抛物线y2=2x的焦点F( ,0),准线方程为x=-
,0),准线方程为x=- ∴在抛物线
∴在抛物线 =2x上任取点P过p作PN⊥直线x=
=2x上任取点P过p作PN⊥直线x= 则PN=
则PN=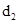
∴根据抛物线的定义可得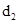 =PF,∴
=PF,∴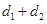 =PM+PF,∵PM+PF
=PM+PF,∵PM+PF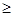 MF,∴当P,M,F三点共线时d1+d2取最小值,此时MF所在的直线方程为y-
MF,∴当P,M,F三点共线时d1+d2取最小值,此时MF所在的直线方程为y- =
= (x-3)即4x-3y-2=0,令4x-3y-2=0,
(x-3)即4x-3y-2=0,令4x-3y-2=0, =2x,联立方程组得到 x-=2,y=2,即当点的坐标为(2,2)时,
=2x,联立方程组得到 x-=2,y=2,即当点的坐标为(2,2)时,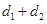 取最小值,故选C
取最小值,故选C
考点:抛物线的性质
点评:本题主要考察抛物线的性质,属常考题,较难.解题的关键是将d1+d2=PM+PN根据抛物线的定义转化为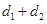 =PM+PF.
=PM+PF.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:单选题
北京奥运会主体育场“鸟巢”的简化钢结构俯视图如图所示,内外两圈的钢骨架是离心率相同的椭圆,从外层椭圆顶点A、B向内层椭圆引切线AC、BD设内层椭圆方程为 +
+ =1(a
=1(a b
b 0),外层椭圆方程为
0),外层椭圆方程为 +
+ =1(a
=1(a b
b 0,m
0,m 1),AC与BD的斜率之积为-
1),AC与BD的斜率之积为- ,则椭圆的离心率为( )
,则椭圆的离心率为( )
A. B.
B. C.
C.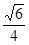 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com