
【题目】如图,在三棱锥P-ABC中,PA⊥底面ABC,AC⊥BC,H为PC的中点,M为AH中点,PA=AC=2,BC=1.
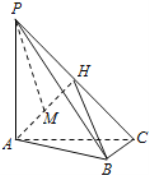
(Ⅰ)求证:AH⊥平面PBC;
(Ⅱ)求PM与平面AHB成角的正弦值;
(Ⅲ)在线段PB上是否存在点N,使得MN∥平面ABC,若存在,请说明点N的位置,若不存在,请说明理由.
【答案】(Ⅰ)见证明;(Ⅱ)![]() (Ⅲ)点N是靠近B点的四等分点
(Ⅲ)点N是靠近B点的四等分点
【解析】
(Ⅰ)根据线面垂直判定与性质定理进行论证,(Ⅱ)先根据条件建立空间直角坐标系,设立各点坐标,列方程组解得平面AHB的一个法向量,根据向量数量积求向量夹角,最后根据向量夹角与线面角关系得结果,(Ⅲ)先设N坐标,再根据![]() 与平面ABC的法向量的数量积为零解得结果.
与平面ABC的法向量的数量积为零解得结果.
(Ⅰ)证明:∵PA⊥底面ABC,
∴PA⊥BC,
又∵AC⊥BC,PA∩AC=A,
∴BC⊥平面PAC,
∵AH平面PAC,
∴BC⊥AH.
∵H为PC的中点,PA=AC,
∴AH⊥PC.
∵PC∩BC=C.
∴AH⊥平面PBC;
(Ⅱ)
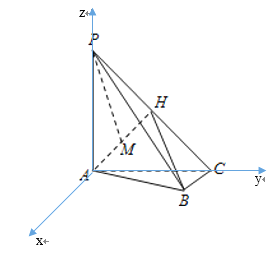
由题意建立空间直角坐标系.A(0,0,0),B(1,2,0),C(0,2,0),
P(0,0,2),H(0,1,1),M![]() .
.
![]() =(0,1,1),
=(0,1,1),![]() =(1,2,0),
=(1,2,0),![]() =
=![]() .
.
设平面ABH的法向量为![]() =(x,y,z),则
=(x,y,z),则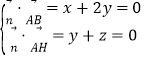 ,取
,取![]() =(2,-1,1).
=(2,-1,1).
设PM与平面AHB成角为![]() ,
,
则sin![]() =
=![]() =
=![]() =
=![]() =
=![]() .
.
所以PM与平面AHB成角的正弦值为![]()
(Ⅲ)假设在线段PB上存在点N,使得MN∥平面ABC.
设![]() ,
,![]() =(1,2,-2),
=(1,2,-2),
∴![]() .
.
∴![]() =
=![]() =
=![]() ,
,
∵MN∥平面ABC,平面ABC的法向量为![]() =(0,0,2),
=(0,0,2),
∴![]() =
=![]() -
-![]() =0,解得
=0,解得![]() .
.
∴点N是靠近B点的四等分点.


科目:高中数学 来源: 题型:
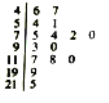
【题目】空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;大于300为严重污染.某环保人士从当地某年的AQI记录数据中,随机抽取了15天的AQI数据,用如图所示的茎叶图记录.根据该统计数据,估计此地该年空气质量为优或良的天数约为__________.(该年为366天)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 是
是![]() 的顶点,
的顶点,![]() ,
,![]() ,直线
,直线![]() ,
,![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设四边形![]() 的顶点都在曲线
的顶点都在曲线![]() 上,且
上,且![]() ,直线
,直线![]() ,
,![]() 分别过点
分别过点![]() ,
,![]() ,求四边形
,求四边形![]() 的面积为
的面积为![]() 时,直线
时,直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名同学在本学期的六次考试成绩统计如图,甲、乙两组数据的平均值分别为![]()
![]() ,则( )
,则( )
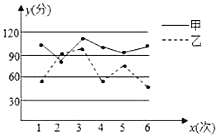
A.每次考试甲的成绩都比乙的成绩高B.甲的成绩比乙稳定
C.![]() 一定大于
一定大于![]() D.甲的成绩的极差大于乙的成绩的极差
D.甲的成绩的极差大于乙的成绩的极差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(I)求椭圆的标准方程;
(II)四边形ABCD的顶点在椭圆上,且对角线AC,BD过原点O,设![]() ,满足
,满足![]() .
.
(i)试证![]() 的值为定值,并求出此定值;
的值为定值,并求出此定值;
(ii)试求四边形ABCD面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),其中
为参数),其中![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,与
,与![]() 交于
交于![]() 两点,且
两点,且![]() ,求
,求![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在圆柱![]() 中,点
中,点![]() 、
、![]() 分别为上、下底面的圆心,平面
分别为上、下底面的圆心,平面![]() 是轴截面,点
是轴截面,点![]() 在上底面圆周上(异于
在上底面圆周上(异于![]() 、
、![]() ),点
),点![]() 为下底面圆弧
为下底面圆弧![]() 的中点,点
的中点,点![]() 与点
与点![]() 在平面
在平面![]() 的同侧,圆柱
的同侧,圆柱![]() 的底面半径为1,高为2.
的底面半径为1,高为2.
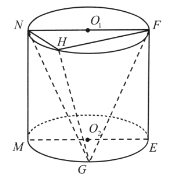
(1)若平面![]() 平面
平面![]() ,证明:
,证明:![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成线面角
所成线面角![]() 的正弦值等于
的正弦值等于![]() ,证明:平面
,证明:平面![]() 与平面
与平面![]() 所成锐二面角的平面角大于
所成锐二面角的平面角大于![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱锥![]() 中,
中,![]() 与
与![]() 都是边长为2的等边三角形,
都是边长为2的等边三角形,![]() 、
、![]() 、
、![]() 、
、![]() 分别是棱
分别是棱![]() 、
、![]() 、
、![]() 、
、![]() 的中点.
的中点.
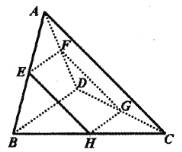
(1)证明:四边形![]() 为矩形;
为矩形;
(2)若平面![]() 平面
平面![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com