
6个人进两间屋子,①每屋都进3人;②每屋至少进1人,问:各有多少种分配方法?
科目:高中数学 来源: 题型:解答题
规定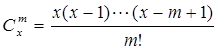 ,其中
,其中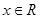 ,
, 是正整数,且
是正整数,且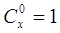 ,这是组合数
,这是组合数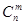 (
( 、
、 是正整数,且
是正整数,且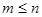 )的一种推广.如当
)的一种推广.如当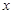 =-5时,
=-5时,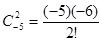
(1)求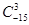 的值;
的值;
(2)设x>0,当x为何值时,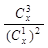 取得最小值?
取得最小值?
(3)组合数的两个性质;
①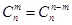 . ②
. ② .
.
是否都能推广到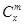 (
(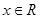 ,
, 是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知非空有限实数集S的所有非空子集依次记为S1,S2,S3, ,集合Sk中所有元素的平均
值记为bk.将所有bk组成数组T:b1,b2,b3, ,数组T中所有数的平均值记为m(T).
(1)若S={1,2},求m(T);
(2)若S={a1,a2, ,an}(n∈N*,n≥2),求m(T).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设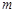 是给定的正整数,有序数组(
是给定的正整数,有序数组(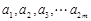 )中
)中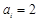 或
或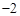
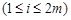 .
.
(1)求满足“对任意的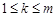 ,
,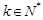 ,都有
,都有 ”的有序数组(
”的有序数组(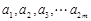 )的个数
)的个数 ;
;
(2)若对任意的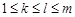 ,
,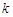 ,
, ,都有
,都有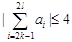 成立,求满足“存在
成立,求满足“存在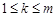 ,使得
,使得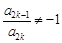 ”的有序数组(
”的有序数组(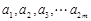 )的个数
)的个数 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
高三某班有两个数学课外兴趣小组,第一组有 名男生,
名男生, 名女生,第二组有
名女生,第二组有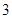 名男生,
名男生, 名女生.现在班主任老师要从第一组选出
名女生.现在班主任老师要从第一组选出 人,从第二组选出
人,从第二组选出 人,请他们在班会上和全班同学分享学习心得.
人,请他们在班会上和全班同学分享学习心得.
(Ⅰ)求选出的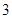 人均是男生的概率;
人均是男生的概率;
(Ⅱ)求选出的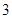 人中有男生也有女生的概率.
人中有男生也有女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com