
设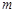 是给定的正整数,有序数组(
是给定的正整数,有序数组(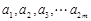 )中
)中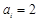 或
或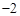
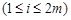 .
.
(1)求满足“对任意的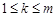 ,
,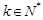 ,都有
,都有 ”的有序数组(
”的有序数组(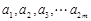 )的个数
)的个数 ;
;
(2)若对任意的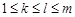 ,
,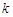 ,
, ,都有
,都有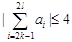 成立,求满足“存在
成立,求满足“存在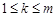 ,使得
,使得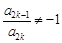 ”的有序数组(
”的有序数组(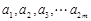 )的个数
)的个数 .
.
(1)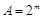 ,(2)
,(2)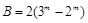 .
.
解析试题分析:
(1)正确理解每一偶数项与前相邻奇数项是相反数,而与后相邻奇数项相等或相反;因此分组按(奇、偶)分为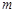 组,每组有2种可能,各组可能互不影响,共有
组,每组有2种可能,各组可能互不影响,共有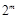 种可能,
种可能,
(2)在(1)的基础上,某些组可能为(2,2)或(-2,-2),需讨论这些组个数的情况,最少一个,最多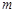 个.另外条件“对任意的
个.另外条件“对任意的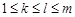 ,
,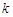 ,
, ,都有
,都有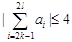 成立”控制不能出现各组都为2或-2的情况,而是间隔出现(2,2)、(-2,-2).
成立”控制不能出现各组都为2或-2的情况,而是间隔出现(2,2)、(-2,-2).
试题解析:
解:(1)因为对任意的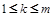 ,都有
,都有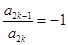 ,则
,则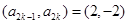 或
或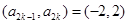
共有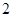 种,所以
种,所以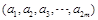 共有
共有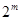 种不同的选择,所以
种不同的选择,所以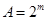 . 5分
. 5分
(2)当存在一个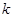 时,那么这一组有
时,那么这一组有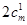 种,其余的由(1)知有
种,其余的由(1)知有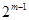 ,所有共有
,所有共有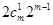 ;
;
当存在二个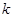 时,因为条件对任意的
时,因为条件对任意的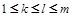 ,都有
,都有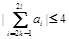 成立得这两组共有
成立得这两组共有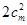 ,
,
其余的由(1)知有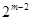 ,所有共有
,所有共有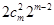 ;
;
依次类推得: . 10分
. 10分
考点:分步(乘法)计数原理,二项式定理应用.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
已知 的展开式的二项式系数的和比(3x-1)n的展开式的二项式系数和大992,求(2x-
的展开式的二项式系数的和比(3x-1)n的展开式的二项式系数和大992,求(2x-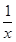 )2n的展开式中,(1)二项式系数最大的项;(2)系数的绝对值最大的项.
)2n的展开式中,(1)二项式系数最大的项;(2)系数的绝对值最大的项.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某医院有内科医生12名,外科医生8名,现选派5名参加赈灾医疗队,其中
(1)某内科医生甲与某外科医生乙必须参加,共有多少种不同选法?
(2)甲、乙均不能参加,有多少种选法?
(3)甲、乙两人至少有一人参加,有多少种选法?
(4)队中至少有一名内科医生和一名外科医生,有几种选法?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com