
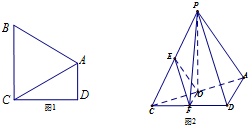
 如图1,在直角梯形ABCD中,AD∥BC,∠ADC=90°,BA=BC=AC=2,把△BAC沿AC折起到△PAC的位置,使得P点在平面ADC上的正投影O恰好落在线段AC上,如图2所示.点E,F分别为棱PC,CD的中点.
如图1,在直角梯形ABCD中,AD∥BC,∠ADC=90°,BA=BC=AC=2,把△BAC沿AC折起到△PAC的位置,使得P点在平面ADC上的正投影O恰好落在线段AC上,如图2所示.点E,F分别为棱PC,CD的中点.分析 (Ⅰ)证明OE∥PA,OF∥AD,利用平面与平面平行的判定定理证明平面OEF∥平面PDA.
(Ⅱ)证明OF⊥CD,PO⊥CD,利用直线与平面垂直的判定定理证明CD⊥平面POF.
(Ⅲ)存在,通过就是$EF=\frac{1}{2}PC$,$EP=EC=OE=\frac{1}{2}PC$,即可证明点M到四个点P,O,C,F的距离相等.
解答 证明:(Ⅰ)因为点P在平面ADC上的正投影O恰好落在线段AC上
所以PO⊥平面ABC,所以PO⊥AC
因为AB=BC,所以O是AC中点,
所以OE∥PA,同理OF∥AD,又OE∩OF=O,PA∩AD=A
所以平面OEF∥平面PDA
(Ⅱ)因为OF∥AD,AD⊥CD,所以OF⊥CD
又PO⊥平面ADC,CD?平面ADC
所以PO⊥CD
又OF∩PO=O
所以CD⊥平面POF
(Ⅲ)存在,事实上记点E为M即可
因为CD⊥平面POF,PF?平面POF
所以CD⊥PF
又E为PC中点,所以$EF=\frac{1}{2}PC$
同理,在直角三角形POC中,$EP=EC=OE=\frac{1}{2}PC$,
所以点M到四个点P,O,C,F的距离相等.
点评 本题考查空间距离公式的应用,直线与平面垂直以及平面与平面垂直与平行的判定定理的应用,考查空间想象能力以及逻辑推理能力.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$,36 | B. | $\frac{2}{3}$,18 | C. | $\frac{1}{6}$,72 | D. | $\frac{1}{2}$,24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com