
���� ��1����������ߵ��߷��̣�������ɵ�p=2c��������Բ�Ķ���ɵ�a=2������ֱ�ߺ������߷��̣������б�ʽΪ0���ɵ�p��b�ķ��̣��ⷽ���飬�ɵ�a=2��p=2��b=$\sqrt{3}$��c=1�������õ������ߺ���Բ���̣�
��2�����ֱ�߷��̣����������ߺ���Բ���̣���ý�������꣬�����������ߵ������ʾ���ⷽ�̿ɵ�k�������õ�����ֱ�߷��̣�
��� �⣺��1��y2=2px��p��0������Ϊx=-$\frac{p}{2}$��
������ɵ�-$\frac{p}{2}$=-c����
����P����Բ������ľ���֮��Ϊ4����Ϊ2a=4��
b2+c2=4����
y=x+$\frac{{b}^{2}}{3}$��������y2=2px�������ɵ�$\frac{1}{2p}$y2-y+$\frac{{b}^{2}}{3}$=0��
�����б�ʽ1-$\frac{2{b}^{2}}{3p}$=0����
�ɢ٢ڢ۽��p=2��b=$\sqrt{3}$��c=1��a=2��
�������ߦ��ķ���Ϊy2=4x����ԲE�ķ���Ϊ$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1��
��2������ֱ��l2��y=kx�������߷���y2=4x���ɵ�A��$\frac{4}{{k}^{2}}$��$\frac{4}{k}$����
����ֱ��l2��y=kx����Բ����$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1��
�ɵ�B��-$\sqrt{\frac{12}{3+4{k}^{2}}}$��-k•$\sqrt{\frac{12}{3+4{k}^{2}}}$����C��$\sqrt{\frac{12}{3+4{k}^{2}}}$��k•$\sqrt{\frac{12}{3+4{k}^{2}}}$����
��$\overrightarrow{BO}$=$\overrightarrow{CA}$���ɵ�$\sqrt{\frac{12}{3+4{k}^{2}}}$=$\frac{4}{{k}^{2}}$-$\sqrt{\frac{12}{3+4{k}^{2}}}$��
���k=$\frac{\sqrt{6+3\sqrt{13}}}{3}$��
����ֱ��l2�ķ���Ϊy=$\frac{\sqrt{6+3\sqrt{13}}}{3}$x��
���� ���⿼����Բ�������ߵĶ��塢���̺����ʣ�����ֱ�ߺ���Բ�������ߵ�λ�ù�ϵ�������������ߵ������ʾ�������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 45�� | B�� | 30�� | C�� | 90�� | D�� | 60�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��λ������ABCD-A1B1C1O�ڿռ�ֱ������ϵ�е�λ����ͼ��ʾ������M��a��a��0����N��0��b��1��������0��a��1��0��b��1������M��N��O����ȷ����ƽ��ظ�������Ľ���ΪE����ô��������
��λ������ABCD-A1B1C1O�ڿռ�ֱ������ϵ�е�λ����ͼ��ʾ������M��a��a��0����N��0��b��1��������0��a��1��0��b��1������M��N��O����ȷ����ƽ��ظ�������Ľ���ΪE����ô��������| A�� | �������M�����ڵ�Nʹ����EΪ������ | |
| B�� | �������M�����ڵ�Nʹ����EΪ������ | |
| C�� | �������M��N������E�������� | |
| D�� | �������N�����ڵ�Mʹ�ý���EΪ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
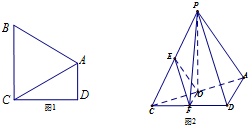 ��ͼ1����ֱ������ABCD�У�AD��BC����ADC=90�㣬BA=BC=AC=2���ѡ�BAC��AC����PAC��λ�ã�ʹ��P����ƽ��ADC�ϵ���ͶӰOǡ�������߶�AC�ϣ���ͼ2��ʾ����E��F�ֱ�Ϊ��PC��CD���е㣮
��ͼ1����ֱ������ABCD�У�AD��BC����ADC=90�㣬BA=BC=AC=2���ѡ�BAC��AC����PAC��λ�ã�ʹ��P����ƽ��ADC�ϵ���ͶӰOǡ�������߶�AC�ϣ���ͼ2��ʾ����E��F�ֱ�Ϊ��PC��CD���е㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com