
【题目】已知椭圆![]() ,右顶点
,右顶点![]() ,上顶点为B,左右焦点分别为
,上顶点为B,左右焦点分别为![]() ,且
,且![]() ,过点A作斜率为
,过点A作斜率为![]() 的直线l交椭圆于点D,交y轴于点E.
的直线l交椭圆于点D,交y轴于点E.
(1)求椭圆C的方程;
(2)设P为![]() 的中点,是否存在定点Q,对于任意的
的中点,是否存在定点Q,对于任意的![]() 都有
都有![]() ?若存在,求出点Q;若不存在,请说明理由.
?若存在,求出点Q;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知定点![]() ,点A在x轴的非正半轴上运动,点B在y轴上运动,满足
,点A在x轴的非正半轴上运动,点B在y轴上运动,满足![]() ,A关于点B的对称点为M,设点M的轨迹为曲线C.
,A关于点B的对称点为M,设点M的轨迹为曲线C.
(1)求C的方程;
(2)已知点![]() ,动直线
,动直线![]() 与C相交于P,Q两点,求过G,P,Q三点的圆在直线
与C相交于P,Q两点,求过G,P,Q三点的圆在直线![]() 上截得的弦长的最小值.
上截得的弦长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,AA1![]() AB
AB![]() AC
AC![]() 2,AB⊥AC,M是棱BC的中点点P在线段A1B上.
2,AB⊥AC,M是棱BC的中点点P在线段A1B上.
(1)若P是线段A1B的中点,求直线MP与直线AC所成角的大小;
(2)若![]() 是
是![]() 的中点,直线
的中点,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段BP的长度.
,求线段BP的长度.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】各项为正数的数列![]() 如果满足:存在实数
如果满足:存在实数![]() ,对任意正整数n,
,对任意正整数n,![]() 恒成立,且存在正整数n,使得
恒成立,且存在正整数n,使得![]() 或
或![]() 成立,则称数列
成立,则称数列![]() 为“紧密数列”,k称为“紧密数列”
为“紧密数列”,k称为“紧密数列”![]() 的“紧密度”.已知数列
的“紧密度”.已知数列![]() 的各项为正数,前n项和为
的各项为正数,前n项和为![]() ,且对任意正整数n,
,且对任意正整数n,![]() (A,B,C为常数)恒成立.
(A,B,C为常数)恒成立.
(1)当![]() ,
,![]() ,
,![]() 时,
时,
①求数列![]() 的通项公式;
的通项公式;
②证明数列![]() 是“紧密度”为3的“紧密数列”;
是“紧密度”为3的“紧密数列”;
(2)当![]() 时,已知数列
时,已知数列![]() 和数列
和数列![]() 都为“紧密数列”,“紧密度”分别为
都为“紧密数列”,“紧密度”分别为![]() ,
,![]() ,且
,且![]() ,
,![]() ,求实数B的取值范围.
,求实数B的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数y=f1(x)的图象以原点为顶点且过点(1,1),反比例函数y=f2(x)的图象与直线y=x的两个交点间距离为8,f(x)= f1(x)+ f2(x).
(Ⅰ) 求函数f(x)的表达式;
(Ⅱ) 证明:当a>3时,关于x的方程f(x)= f(a)有三个实数解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=3,直线PA与圆O相切于点A,直线PB垂直y轴于点B,且|PB|=2|PA|.
(1)求点P的轨迹E的方程;
(2)过点(1,0)且与x轴不重合的直线与轨迹E相交于P,Q两点,在x轴上是否存在定点D,使得x轴是∠PDQ的角平分线,若存在,求出D点坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
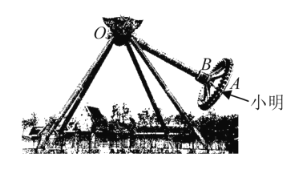
【题目】如图,大摆锤是一种大型游乐设备,常见于各大游乐园.游客坐在圆形的座舱中,面向外.通常大摆锤以压肩作为安全束缚,配以安全带作为二次保险.座舱旋转的同时,悬挂座舱的主轴在电机的驱动下做单摆运动.今年五一,小明去某游乐园玩“大摆锤”,他坐在点A处,“大摆锤”启动后,主轴![]() 在平面
在平面![]() 内绕点O左右摆动,平面
内绕点O左右摆动,平面![]() 与水平地面垂直,
与水平地面垂直,![]() 摆动的过程中,点A在平面
摆动的过程中,点A在平面![]() 内绕点B作圆周运动,并且始终保持
内绕点B作圆周运动,并且始终保持![]() ,
,![]() .已知
.已知![]() ,在“大摆锤”启动后,给出下列结论:
,在“大摆锤”启动后,给出下列结论:
①点A在某个定球面上运动;
②线段![]() 在水平地面上的正投影的长度为定值;
在水平地面上的正投影的长度为定值;
③直线![]() 与平面
与平面![]() 所成角的正弦值的最大值为
所成角的正弦值的最大值为![]() ;
;
④![]() 与水平地面所成角记为
与水平地面所成角记为![]() ,直线
,直线![]() 与水平地面所成角记为
与水平地面所成角记为![]() ,当
,当![]() 时,
时,![]() 为定值.
为定值.
其中正确结论的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂能够生产甲、乙两种产品,已知生产这两种产品每吨所需的煤、电以及每吨的产值分别是:
用煤(t) | 用电(kw) | 产值(千元) | |
甲种产品 | 70 | 20 | 80 |
乙种产品 | 30 | 50 | 110 |
如果该厂每月至多供煤560t,供电450kw,问如何安排生产,才能使该厂月产值最大?月产值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com