
【题目】已知函数![]()
(1)若![]() ,方程
,方程![]() 的实根个数不少于2个,证明:
的实根个数不少于2个,证明:![]()
(2)若![]() 在
在![]() ,
,![]() 处导数相等,求
处导数相等,求![]() 的取值范围,使得对任意的
的取值范围,使得对任意的![]() ,
,![]() ,恒有
,恒有![]() 成立.
成立.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据导数求出函数的单调性及最值,分析函数的大致图象,即可求出满足条件的![]() 的取值范围;
的取值范围;
(2)先由题意知![]() 在
在![]() 不单调得
不单调得![]() ,分
,分![]() 与
与![]() 两种情况,研究
两种情况,研究![]() 的最大值,从而得证.
的最大值,从而得证.
(1)函数![]() 的导函数为:
的导函数为:![]() .
.
函数![]() 的导函数为:
的导函数为:![]() .
.
![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
![]() 时
时![]() ,
,![]() 单调递减
单调递减
因为![]() 时
时![]() ,
,![]() 时
时![]() .
.![]()
所以![]() 有两个不同的实数根
有两个不同的实数根![]() ,
,![]() (其中
(其中![]() ).
).
![]() 时
时![]() ,即
,即![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递减;
上单调递减;
![]() 时
时![]() ,即
,即![]() 在
在![]() 上单调递增.
上单调递增.
又因为![]() 时
时![]() ,
,![]() 时
时![]() ,
,
所以,![]()
故![]() 即有实根个数不少于2个
即有实根个数不少于2个
由题意得,![]() .
.
因为![]() ,所以
,所以![]() .
.
故![]() .
.
(2)函数![]() 的导函数
的导函数![]() .
.
由题意得,![]() 在
在![]() 不单调
不单调
所以,![]()
函数![]() 的导函数为:
的导函数为:![]() .
.
又![]() 时
时![]() ,
,![]() 单调递增:
单调递增:![]() 时
时![]() ,
,![]() 单调递减
单调递减
所以a的取值范围是![]()
因为![]() 时
时![]() ,
,![]() 时
时![]() .
.
所以![]() ,
,![]() .
.
由![]() 得,
得,![]() .
.
而![]() ,其中
,其中![]() .
.
设![]() ,
,![]() ,函数
,函数![]() 的导函数
的导函数
 .即
.即![]() 在
在![]() 上单调递增
上单调递增
所以,![]() .即
.即![]() .
.
因此,![]() .
.
故![]() .即
.即![]() 在
在![]() 上单调递减.
上单调递减.
若![]() ,则
,则
![]() .即
.即![]() 在
在![]() 上单调递减.
上单调递减.
所以![]()
若![]() ,因为
,因为![]() ,所以必有
,所以必有![]() ,使得当
,使得当![]() 时,
时,![]()
即![]() 在
在![]() 上单调递增,这与
上单调递增,这与![]() 恒成立矛盾.
恒成立矛盾.
综上,![]() .(开闭区间不作要求)
.(开闭区间不作要求)


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为坐标原点,过点
为坐标原点,过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)若直线![]() 与圆
与圆![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,且
,且![]() ,
,![]() ,试探究:
,试探究:![]() 是否为定值.若为定值,求出该定值,若不为定值,试说明理由.
是否为定值.若为定值,求出该定值,若不为定值,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆方程为![]() .
.
(1)设椭圆的左右焦点分别为![]() 、
、![]() ,点
,点![]() 在椭圆上运动,求
在椭圆上运动,求![]() 的值;
的值;
(2)设直线![]() 和圆
和圆![]() 相切,和椭圆交于
相切,和椭圆交于![]() 、
、![]() 两点,
两点,![]() 为原点,线段
为原点,线段![]() 、
、![]() 分别和圆
分别和圆![]() 交于
交于![]() 、
、![]() 两点,设
两点,设![]() 、
、![]() 的面积分别为
的面积分别为![]() 、
、![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
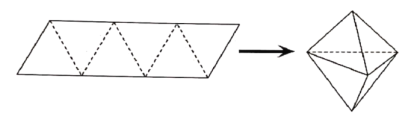
【题目】农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,俗称粽子,古称“角黍”,是端午节大家都会品尝的食品,传说这是为了纪念战国时期的楚国大臣、爱国主义诗人屈原.如图,平行四边形形状的纸片是由六个边长为2的正三角形组成的,将它沿虚线对折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为______________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,右顶点
,右顶点![]() ,上顶点为B,左右焦点分别为
,上顶点为B,左右焦点分别为![]() ,且
,且![]() ,过点A作斜率为
,过点A作斜率为![]() 的直线l交椭圆于点D,交y轴于点E.
的直线l交椭圆于点D,交y轴于点E.
(1)求椭圆C的方程;
(2)设P为![]() 的中点,是否存在定点Q,对于任意的
的中点,是否存在定点Q,对于任意的![]() 都有
都有![]() ?若存在,求出点Q;若不存在,请说明理由.
?若存在,求出点Q;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆周率π是数学中一个非常重要的数,历史上许多中外数学家利用各种办法对π进行了估算.现利用下列实验我们也可对圆周率进行估算.假设某校共有学生N人,让每人随机写出一对小于1的正实数a,b,再统计出a,b,1能构造锐角三角形的人数M,利用所学的有关知识,则可估计出π的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,右顶点
,右顶点![]() ,上顶点为B,左右焦点分别为
,上顶点为B,左右焦点分别为![]() ,且
,且![]() ,过点A作斜率为
,过点A作斜率为![]() 的直线l交椭圆于点D,交y轴于点E.
的直线l交椭圆于点D,交y轴于点E.
(1)求椭圆C的方程;
(2)设P为![]() 的中点,是否存在定点Q,对于任意的
的中点,是否存在定点Q,对于任意的![]() 都有
都有![]() ?若存在,求出点Q;若不存在,请说明理由.
?若存在,求出点Q;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() .
.
(1)求曲线C的极坐标方程和直线l的直角坐标方程;
(2)若射线![]() 与曲线C交于点A(不同于极点O),与直线l交于点B,求
与曲线C交于点A(不同于极点O),与直线l交于点B,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com