
(本小题满分13分)已知平面 平面
平面 ,四边形
,四边形 是矩形,
是矩形, ,
,  、
、 分别是
分别是 、
、 的中点,主(正)视图方向垂直平面
的中点,主(正)视图方向垂直平面 时,左(侧)视图的面积为
时,左(侧)视图的面积为 .
.

(1)求证: ∥平面
∥平面 ;
;
(2)求证:平面
 平面
平面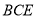 .
.
(1)(2)答案见解析.
【解析】
试题分析:(1)依题意取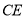 的中点
的中点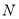 ,连接
,连接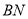 ,MN ,易得MN||CD且
,MN ,易得MN||CD且 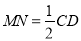 而
而 ∥
∥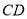 且
且 =
=
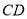 故
故 ∥
∥ 且
且 =
= 得四边形
得四边形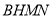 为平行四边形,
为平行四边形,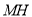 ∥
∥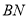 ,由线面平行的判定定理知
,由线面平行的判定定理知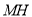 ∥平面
∥平面 ; (2)取
; (2)取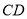 中点
中点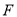 ,连接
,连接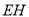 、
、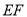 、
、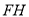 ,则几何体的左视图即为
,则几何体的左视图即为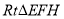 ,从而可得
,从而可得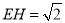 ,由勾股定理可得
,由勾股定理可得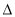
 为
为 ,∴
,∴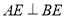 ,又已知平面
,又已知平面 平面
平面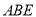 ,四边形
,四边形 是矩形易得
是矩形易得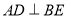 ,从而
,从而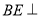 平面
平面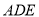 ,故可证平面
,故可证平面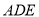
 平面
平面 .
.
试题解析:(1)证明:方法一、取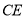 的中点
的中点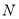 ,连接
,连接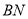 ,
,
因为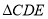 中,
中, 、
、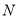 分别是
分别是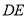 、
、 的中点,
的中点,
所以 ∥
∥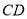 且
且 =
=
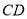 ; 1分
; 1分
因为矩形 中,
中,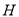 是
是 的中点,
的中点, ∥
∥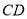 且
且 =
=
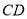 ;
;
所以 ∥
∥ 且
且 =
= ,得平行四边形
,得平行四边形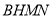 ,
,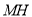 ∥
∥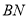 2分
2分
因为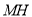
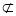 平面
平面 ,
,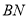
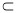 平面
平面 ,所以
,所以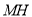 ∥平面
∥平面 ; 4分
; 4分
方法二、取 的中点
的中点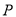 ,连接
,连接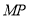 、
、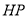 ,
,
因为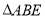 中,
中,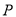 、
、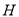 分别是
分别是 、
、 的中点,所以
的中点,所以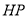 ∥
∥ ,
,
因为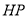
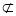 平面
平面 ,
, 
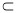 平面
平面 ,所以
,所以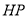 ∥平面
∥平面 ; 1分
; 1分
同理可证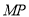 ∥平面
∥平面 ; 2分
; 2分
因为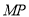
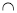
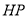 =
=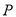 ,所以平面
,所以平面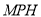 ∥平面
∥平面 ; 3分
; 3分
因为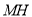
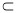 平面
平面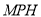 ,所以
,所以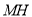 ∥平面
∥平面 ; 4分
; 4分

(2)证明:取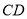 中点
中点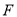 ,连接
,连接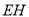 、
、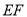 、
、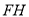 ,
,
则矩形 中,
中,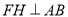 ,
,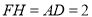 , 5分
, 5分
因为 中
中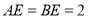 ,所以
,所以 ,
,
因为平面 平面
平面 ,交线为
,交线为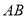 ,所以
,所以 平面
平面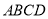 ,
,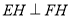 ,
,
所以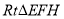 的面积等于几何体
的面积等于几何体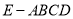 左(侧)视图的面积,得
左(侧)视图的面积,得
 即
即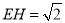 ; 8分
; 8分
所以 中,
中,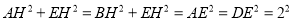 ,
, ,
,
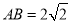 ,
,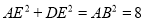 ,
,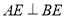 ; 10分
; 10分
因为平面 平面
平面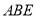 ,四边形
,四边形 是矩形,所以
是矩形,所以 平面
平面 ,
,
因为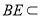 平面
平面 ,所以
,所以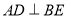 ; 11分
; 11分
因为 ,所以
,所以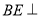 平面
平面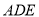 ; 12分
; 12分
因为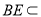 平面
平面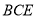 ,所以平面
,所以平面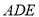
 平面
平面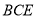 . 13分
. 13分
考点:空间直线与平面、平面与平面的位置关系


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014-2015学年湖北鄂州泽林中学高二上第一次月考理科数学试卷(解析版) 题型:选择题
在下列说法中,正确的是( )
A.在循环结构中,直到型先判断条件,再执行循环体,当型先执行循环体,后判断条件
B.互斥事件一定是对立事件,对立事件不一定是互斥事件
C.从含有2008个个体的总体中抽取一个容量为100的样本,现采用系统抽样方法应先剔除8人,则每个个体被抽到的概率均为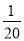
D.如果将一组数据中的每一个数都加上同一个非零常数,那么这组数据的平均数改变,方差不变
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北鄂州泽林中学高二上第一次月考文科数学试卷(解析版) 题型:选择题
在△ABC中,角A,B,C所对的边分别为a,b,c. 若 ,
, ,
, ,则
,则 ( )
( )
(A) (B)
(B) (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北襄阳襄州一中等四校高二上学期期中文科数学试卷(解析版) 题型:填空题
如图所示的算法中, ,
, ,
, ,其中
,其中 是圆周率,
是圆周率, 是自然对数的底数,则输出的结果是 .
是自然对数的底数,则输出的结果是 .

查看答案和解析>>
科目:高中数学 来源:2015届吉林省高二下学期期中考试文科数学试卷(解析版) 题型:选择题
设点 对应的复数为
对应的复数为 ,以原点为极点,实轴正半轴为极轴建立极坐标系,
,以原点为极点,实轴正半轴为极轴建立极坐标系,
则点 的极坐标可能为( )
的极坐标可能为( )
A. (3, ) B. (3,
) B. (3, ) C. (
) C. ( ,
, ) D. (
) D. ( ,
, )
)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北襄阳襄州一中等四校高二上学期期中文科数学试卷(解析版) 题型:选择题
第三赛季甲、乙两名运动员每场比赛得分的茎叶图如图所示,则下列说法中正确的是( )

A.甲、乙两人单场得分的最高分都是9分;
B.甲、乙两人单场得分的中位数相同;
C.甲运动员的得分更集中,发挥更稳定;
D.乙运动员的得分更集中,发挥更稳定.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省高二上学期期中考试理科数学试卷(解析版) 题型:选择题
对两个变量 和
和 进行回归分析,得到一组样本数据:
进行回归分析,得到一组样本数据: ,
, ,…,
,…, ,则下列说法中不正确的是( )
,则下列说法中不正确的是( )
A.由样本数据得到的回归方程 必过样本中心
必过样本中心
B.残差平方和越小的模型,拟合的效果越好
C.用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好
D.若变量 和
和 之间的相关系数为
之间的相关系数为 ,则变量
,则变量 和
和 之间具有线性相关关系
之间具有线性相关关系
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com