
| A. | c<a<b | B. | a<b<c | C. | b<a<c | D. | a<c<b |
分析 由题意,构造函数g(x)=$\frac{f(x)}{x-1}$,利用已知判断其单调性,利用单调性得到所求.
解答 解:由题意,构造函数g(x)=$\frac{f(x)}{x-1}$,所以g'(x)=$\frac{(x-1)f'(x)-f(x)}{(x-1)^{2}}$,因为当x∈(1,+∞)时,(x-1)f′(x)-f(x)>0恒成立,
所以g'(x)>0在x∈(1,+∞)恒成立,所以函数g(x)在x∈(1,+∞)为增函数,又$\sqrt{3}$<2<3,
所以g($\sqrt{3}$)<g(2)<g(3)即$\frac{1}{\sqrt{3}-1}$f($\sqrt{3}$)<f(2)<$\frac{1}{2}$f(3);所以c<a<b;
故选A.
点评 本题考查了构造函数的思想以及利用函数的大小判断函数值的大小;属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 对一批电子元件进行寿命追踪调查,从这批产品中抽取N个产品(其中N≥200),得到频率分布直方图如表:
对一批电子元件进行寿命追踪调查,从这批产品中抽取N个产品(其中N≥200),得到频率分布直方图如表:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>1 | B. | a<-1 | C. | a>2 | D. | a<-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
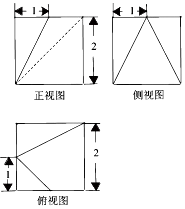
| A. | 8 | B. | 7 | C. | $\frac{23}{3}$ | D. | $\frac{22}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com