
分析 由am+n=am•an,令m等于1化简后,由等比数列的定义确定此数列是等比数列,利用等比数列的前n项和的公式表示出Sn,利用极限思想和条件求出满足条件a的范围,再求出a的最小值
解答 解:由题意得,对任意正整数m,n,都有am+n=am•an,
令m=1,得到an+1=a1•an,则$\frac{{a}_{n+1}}{{a}_{n}}$=a1=$\frac{1}{3}$,
则数列{an}是首项、公比都为$\frac{1}{3}$的等比数列,
∴Sn=$\frac{\frac{1}{3}[1-(\frac{1}{3})^{n}]}{1-\frac{1}{3}}$=$\frac{1}{2}$-$\frac{1}{2}$($\frac{1}{3}$)n<$\frac{1}{2}$,
因为Sn<a对任意n∈N*恒成立,所以a≥$\frac{1}{2}$,则实数a的最小值是$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题考查了等比数列关系的确定,等比数列的前n项和的公式,以及不等式恒成立问题,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{1}{5}$个单位长度 | B. | 向右平移$\frac{π}{5}$个单位长度 | ||
| C. | 向右平移$\frac{1}{5}$个单位长度 | D. | 向左平移$\frac{π}{5}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
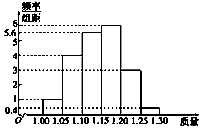 为了了解一个小水库中养殖的鱼的有关情况,从这个水库中多个不同位置捕捞出100条鱼,称得每条鱼的质量(单位:kg),并将所得数据分组,画出频率分布直方图(如图所示).
为了了解一个小水库中养殖的鱼的有关情况,从这个水库中多个不同位置捕捞出100条鱼,称得每条鱼的质量(单位:kg),并将所得数据分组,画出频率分布直方图(如图所示).| 分组 | 频率 |
| [1.00,1.05) | |
| [1.05,1.10) | |
| [1.10,1.15) | |
| [1.15,1.20) | |
| [1.20,1.25) | |
| [1.25,1.30) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com