练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．为了得到函数$y=cos（x+\frac{π}{5}）$，x∈R的图象，只需把余弦曲线y=cosx上的所有的点（　　）
    A．向左平移$\frac{1}{5}$个单位长度B．向右平移$\frac{π}{5}$个单位长度
    C．向右平移$\frac{1}{5}$个单位长度D．向左平移$\frac{π}{5}$个单位长度

    分析 根据函数y=Asin（ωx+φ）的图象变换规律，可得结论．

    解答 解：把余弦曲线y=cosx上的所有的点向左平移$\frac{π}{5}$个单位长度，
    可得函数y=cos（x+$\frac{π}{5}$）的图象，
    故选：D．

    点评 本题主要考查函数y=Asin（ωx+φ）的图象变换规律，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2016-2017学年河南省新乡市高二上学期入学考数学卷（解析版） 题型：选择题

    某公司有1000名员工．其中高层管理人员为50名，属于高收入者；中层管理人员为150名，属于中等收入者；一般员工800名，属于低收入者．要对该公司员工的收入情况进行调查，欲抽取200名员工进行调查，应从中层管理人员中抽取的人数为

    A．10 B．15 C．20 D．30

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．已知数列{an}，an=（2n+m）+（-1）n（3n-2）（m∈N*，m与n无关），则$\sum_{i=1}^{2m}$a2i-1的最大值为2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．已知角θ的终边过点（4，-3），则cos（π-θ）=-$\frac{4}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．已知直线y=k（x-1）+1与圆C：x2-4x+y2+1=0交于A，B两点，则|AB|的最小值为2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．函数$y=\frac{1}{1-sinx}$的定义域为$\left\{{x\left|{\;}\right.x≠\frac{π}{2}+2kπ，k∈Z}\right\}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

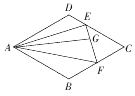    19．如图，在平行四边形ABCD中，$DE=\frac{1}{2}EC$，F为BC的中点，G为EF上的一点，且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$，则实数m的值为（　　）
    A．$\frac{7}{9}$B．$-\frac{2}{9}$C．$-\frac{1}{9}$D．$\frac{5}{9}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．在用反证法证明“在△ABC中，若∠C是直角，则∠A和∠B都是锐角”的过程中，应该假设（　　）
    A．∠A和∠B都不是锐角B．∠A和∠B不都是锐角
    C．∠A和∠B都是钝角D．∠A和∠B都是直角

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．设数列{an}的前n项和为Sn，a1=$\frac{1}{3}$，且对任意m，n∈N*，am+n=am•an，若Sn＜a恒成立，则a的最小值为$\frac{1}{2}$．

    查看答案和解析>>

    同步练习册答案