
【题目】设无穷数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)求数列![]() 的通项公式;
的通项公式;
(3)是否存在数列![]() 的一个无穷子数列
的一个无穷子数列![]() ,使
,使![]() 对一切
对一切![]() 均成立?若存在,请写出数列
均成立?若存在,请写出数列![]() 的所有通项公式;若不存在,请说明理由.
的所有通项公式;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)不存在数列
;(3)不存在数列![]() 的一个无穷子数列
的一个无穷子数列![]() ,使
,使![]() ,对一切
,对一切![]() 均成立..
均成立..
【解析】
(1)令![]() ,则
,则![]() ,解得
,解得![]() .
.
(2)![]() ,
,
![]() ,
,![]() ,
,
两式相减得![]() ,又因为
,又因为![]() ,故数列
,故数列![]() 的首项为1,公差为1的等差数列,所以
的首项为1,公差为1的等差数列,所以![]() ,故
,故![]() .
.
(3)假设存在数列![]() 的一个无穷子数列
的一个无穷子数列![]() ,使
,使![]() 对一切
对一切![]() 均成立,
均成立,
则![]() ,
,
因为![]() 为无穷子数列,则存在
为无穷子数列,则存在![]() 使得
使得
![]() .
.
所以![]() 整理得
整理得![]() ,与
,与![]() 为递增数列矛盾,故假设不成立,
为递增数列矛盾,故假设不成立,
即不存在数列![]() 的一个无穷子数列
的一个无穷子数列![]() ,使
,使![]() ,对一切
,对一切![]() 均成立.
均成立.
(1)令![]() ,
,![]()
(2)![]() ,
,
![]() ,
,![]() ,
,
两式相减得![]() ,
,
整理得![]() ,又因为
,又因为![]() ,
,
故数列![]() 的首项为1,公差为1的等差数列,
的首项为1,公差为1的等差数列,
所以![]() ,故
,故![]() .
.
(3)假设存在数列![]() 的一个无穷子数列
的一个无穷子数列![]() ,使
,使![]() 对一切
对一切![]() 均成立,
均成立,
则![]() ,
,
因为![]() 为无穷子数列,则存在
为无穷子数列,则存在![]() 使得
使得
![]() .
.
所以![]() 整理得
整理得![]() ,
,
由(2)得![]() ,数列
,数列![]() 为数列
为数列![]() 的一个无穷子数列,则
的一个无穷子数列,则![]() 为递增数列,这与
为递增数列,这与![]() 矛盾,故假设不成立,
矛盾,故假设不成立,
即不存在数列![]() 的一个无穷子数列
的一个无穷子数列![]() ,使
,使![]() ,对一切
,对一切![]() 均成立.
均成立.


科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() ,点
,点![]() 满足
满足![]() ,记点
,记点![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)设直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的面积(
的面积(![]() 为坐标原点);
为坐标原点);
(3)设![]() 是线段
是线段![]() 中垂线上的动点,过
中垂线上的动点,过![]() 作
作![]() 的两条切线
的两条切线![]() 、
、![]() ,
,![]() 、
、![]() 分别为切点,判断是否存在定点
分别为切点,判断是否存在定点![]() ,直线
,直线![]() 始终经过点
始终经过点![]() ,若存在,求出点
,若存在,求出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已如椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,
,![]() 为
为![]() 上的动点.
上的动点.
(1)若![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,试用解析式将
,试用解析式将![]() 表示成
表示成![]() 的函数;
的函数;
(2)试根据![]() 的不同取值,讨论满足
的不同取值,讨论满足![]() 为等腰锐角三角形的点
为等腰锐角三角形的点![]() 的个数.
的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “f(0)![]() ”是“函数f(x)是奇函数”的充要条件
”是“函数f(x)是奇函数”的充要条件
B. 若p:![]() ,
,![]() ,则
,则![]() :
:![]() ,
,![]()
C. “若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
D. 若![]() 为假命题,则p,q均为假命题
为假命题,则p,q均为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年反映社会现实的电影《我不是药神》引起了很大的轰动,治疗特种病的创新药研发成了当务之急.为此,某药企加大了研发投入,市场上治疗一类慢性病的特效药品![]() 的研发费用
的研发费用![]() (百万元)和销量
(百万元)和销量![]() (万盒)的统计数据如下:
(万盒)的统计数据如下:
研发费用 | 2 | 3 | 6 | 10 | 13 | 15 | 18 | 21 |
销量 | 1 | 1 | 2 | 2.5 | 3.5 | 3.5 | 4.5 | 6 |
(1)求![]() 与
与![]() 的相关系数
的相关系数![]() 精确到0.01,并判断
精确到0.01,并判断![]() 与
与![]() 的关系是否可用线性回归方程模型拟合?(规定:
的关系是否可用线性回归方程模型拟合?(规定:![]() 时,可用线性回归方程模型拟合);
时,可用线性回归方程模型拟合);
(2)该药企准备生产药品![]() 的三类不同的剂型
的三类不同的剂型![]() ,
,![]() ,
,![]() ,并对其进行两次检测,当第一次检测合格后,才能进行第二次检测.第一次检测时,三类剂型
,并对其进行两次检测,当第一次检测合格后,才能进行第二次检测.第一次检测时,三类剂型![]() ,
,![]() ,
,![]() 合格的概率分别为
合格的概率分别为![]() ,
,![]() ,
,![]() ,第二次检测时,三类剂型
,第二次检测时,三类剂型![]() ,
,![]() ,
,![]() 合格的概率分别为
合格的概率分别为![]() ,
,![]() ,
,![]() .两次检测过程相互独立,设经过两次检测后
.两次检测过程相互独立,设经过两次检测后![]() ,
,![]() ,
,![]() 三类剂型合格的种类数为
三类剂型合格的种类数为![]() ,求
,求![]() 的数学期望.
的数学期望.
附:(1)相关系数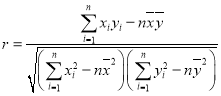
(2)![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.若样本![]() 的平均数为5,标准差为1,则样本
的平均数为5,标准差为1,则样本![]() 的平均数为11,标准差为2
的平均数为11,标准差为2
B.身高和体重具有相关关系
C.现有高一学生30名,高二学生40名,高三学生30名,若按分层抽样从中抽取20名学生,则抽取高三学生6名
D.两个变量间的线性相关性越强,则相关系数的值越大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com